In this section, we look at the idea of having different languages at different levels of the tower---a possibility mentioned in earlier work on reflection [Danvy And Malmkjær 88], but not investigated further there, as, for simplicity in describing reflective interpretation, the languages were taken to be the same at all levels. However, in the Mix system [Jones, Sestoft And Søndergaard 87] the languages are taken to vary between the different programs being mixed together.
Mixed-language systems have been around for a while now, often for specific tasks. They are used when specific features of several languages are all combined. Typically, use of one language is nested within use of another. This may be done as a way of extending an existing language, or as a way of developing a new language without having to develop the parts of it that are already done adequately by an existing one. There are several such language combinations in common use on Unix systems, for example:
Other language systems which in effect combine languages are those in which different areas of one language are so dissimilar that they are handled separately, or are separated for convenience of implementation. Examples of this include:
Such arrangements, being well-established in
practice, have shown themselves to be powerful and
effective. They are, perhaps, examples of the best
tools being selected for particular jobs, making
elegant combined tools available. This may also
take some other forms, such as merging pieces of
assembly-language code in-line in FORTRAN or C
(asm statements) or use of such a feature as
the unix system(2) call, which allows a C
(or other compiled language) program to interpret
a line of shell, which might run any form of
program---either a shell script or a program
in any compiled (or interpreted) language---while
also using the shell's own features, such as
wildcard expansion.
When languages occur in groups or pairs like these, often one of them is being used as a higher-level language than the other---closer to its application domain. For example, in YACC, the YACC parts of the program are a higher-level description of what the program has to do, while the C is used for low-level actions. In many of these cases, the higher-level of the two is also more specific to its application field, and the lower is a relatively general language, for example tbl is specialized for typesetting tables, whereas troff, with which tbl works, is a general-purpose typesetting language.
It is interesting to note that Unix---a system
designed, or allowed to evolve, more on practical
considerations than for abstract theoretical
elegance---includes, in its model of loading and
executing programs, a device for allowing program
files to be interpreted automatically by an
interpreter specified in the file. When a file is
about to be loaded for execution, its first few
bytes are examined for being a particular magic
number (representing the ASCII string \#! or
\#! /). If this is found (instead of the
magic number value that indicates an executable
machine-code file), the program in the file named
in the following bytes of the original file is run
instead, using the original command line arguments
but with the original filename and optional flags
(from the original file) prepended. This
mechanism, originally provided to allow a choice
of shell languages with automatic selection of the
right one for each shell script, allows an
interpreted program (in any language) to be run in
place of a compiled one---with the one restriction
that the interpreted language must allow \#
as a comment character! This is a tower of
interpretation, although one which does not
necessarily provide a program with means to access
itself or its interpreter.
Another way in which mixed-language working is useful is in the provision of libraries of useful routines (for example, numerical algorithms); with cross-language calling being available, a library written in one language (chosen for its suitability for that use) may be used by programs written in any language, thus avoiding the need either for writing a version of the library for (and in) each language from which it is to be used, or for writing an interface library (typically written in assembler) to perform the adaptations from one language's calling protocol to another's. A practical example of this is that the NAG FORTRAN library is now provided with a set of C header files, to enable it to be called directly from C programs.
With truly first-class mixed-language working, there need be no visible seams where routines written in different languages fit together.
Here, we attempt to formalize mixed-language working, and provide a general means for describing languages.
A system in which mixed-language working is available as a first-class feature has several requirements on its design not usually taken into consideration when designing an ordinary, single-language, program execution system.
A common framework for interpretation must be found into which a wide variety of languages may be fitted. At the same time, this framework must be suitable for reification and reflection---programs, program state, and languages must be in forms that can be manipulated readily: everything should be decomposable (or destructurable) to a suitably fine level---for example, it should be possible to extract the representation of a variable binding, a statement in a program, a term in an expression, a construct in a language---and all these representations should be the same in all languages.
There are two areas in this design task: a suitable representation for the static parts of the system---program and interpreter; and one for the dynamic parts---the program's state and the interpreter's state.
It turns out that the most flexible representation for the procedures of a program leads naturally to a representation for languages which has a suitable granularity for picking out individual language constructs and manipulating them. We weave this representation into the basic structure of closures (as described in clochap), and in doing so find a solution to storing the dynamic part of the system: the application data and application state data, which are stored in the variable storage (value list and environment) of the program and its interpreter respectively. This form of data storage fits many languages' models of variable access very well.
Using a program representation based on parse trees and a state representation based on stacks or continuations, our mechanisms can support a wide range of languages. Lisp in some form (Scheme being perhaps the best example [Rees And Clinger 86]) is perhaps the language that is closest to our model---also having the advantage of very little syntax. Scheme is the dialect most commonly used for reflection experiments so far, but the differences are not significant in the examples given. Being a simple representation of a parse tree, a Lisp expression is a convenient way of representing constructs parsed from other languages, and so we use it here as our main language for describing features relevant to languages in general. Since the core of Lisp is a particularly simple language, we will also give special attention to how it maps onto our reflective system, taking it as the primary example language.
Also, Lisp is both a functional language and an
algorithmic one, and thus its structure is able to
receive conveniently mappings from either of these
types of language. The form of Lisp that we use
here includes state-dependent operators such as
while loops, and assignment.
Much of the code given in examples in this thesis could be run on almost any Lisp system; the parts that are not in the languages provided within Platypus are actually Common Lisp [Steele 84].
In our representation, node (expression, or
statement) in the parse tree is identified by its
first element, a leaf (symbol or name, rather than
a further branching sub-tree) which we call the
operator of that node. This is always the case, no
matter how the construct appears in the textual
form of the language. For example, the expression
written in many languages as a + ( b / c )
is stored here in the form (+ a (/ b
c))---its Lisp-like representation.
Different languages map onto this common structure with varying degrees of ease: the model was designed for flexibility, but paradigms of computation vary widely, including pattern replacement languages such as SNOBOL and constraint languages, for example, along with the normal Turing Machines and algorithmic and functional languages.
Mapping Lisp onto our model of interpretation is trivial, since, as explained above, the model is so similar to Lisp.
The block-structured algorithmic languages also fit the model quite well, since their block structure is naturally easy to represent as a parse tree, and our model of interpretation has much in common with them. Those languages, such as Pascal and Algol, which are quite careful about type conversions and coercions fit in cleanly; C, with its freeer typing system, fits the control structure easily, but is not so comfortable on the tagged type system.
The non-block-structured languages such as FORTRAN, COBOL and BASIC can be fitted in, although slightly awkwardly. Their procedures must be written in terms of sequential execution operators which work their way through a series of statements (sub-trees) and which also provide facilities to switch (jump) to specified sub-expressions. (This switching may be done by a separate GOTO operator, or by the sequence operator directly.)
Stack Languages such as FORTH and PostScript fit in as block-structured algorithmic languages; their stack-based data storage is not a significant difference as far as we are concerned, although these languages are not usually regarded as being in the Algol group.
Logic Languages, such as Prolog [Clocksin And Mellish 81], are one of the worst matches to our model; their definitions must be procedurized (as explained in section 8.8) to produce something that we can store in terms of ors, ands and bindings. However, once procedurized, they fit our model of environments well, particularly in how they can then share bindings/instantiations with non logic-based languages, as explained in section 3.1.
One complication that occurs here is backtracking, which may be handled using continuation passing [Jackson]. In the committed-choice variety of logic languages, this problem is obviated by not providing backtracking.
A further problem in interfacing logic languages to other languages (a general problem, not unique to this system) is that logic languages may return a choice of results, rather than a single result. This is part of quite a general difference between families and languages.
Object-Oriented languages, which may be
regarded as a variety of algorithmic language, can
fit this model comfortably, using a closure to
represent each object. The language and
type-evaluators of the closure are then the
method dispatch table for that object. A variety
of object-oriented language that is clearly suited
to constructing this way is the actor
languages described in [Agha 86].
Reflection is commonly associated with object-oriented languages, perhaps largely because of the fame of the reflective object-oriented language SmallTalk80 [Goldberg And Robson 83]. In developing Platypus, I have been careful to avoid an object-based style, to show that reflection and object are entirely separate facilities in a language system.
This thesis is about a system in which languages are values that can be passed around---which inherently has the ability to be a mixed-language system. We have described in section 4.4 a system using one standard interpreter. How can we extend a single interpreter to handle a variety of languages? The ability to do this (and many other benefits) depends on a suitable abstraction for a language interpreter, and constructing that interpreter is a central part of this thesis.
Our abstraction for language interpreters is based
around the parse tree abstraction for procedure
representation. The language is arranged as a
collection of named operators, where the
names of the operators are those that appear in
the nodes of the parse tree, and the definitions
referred to by those names are the closures of
the procedures used to implement each named
language construct. Thus, a language---as we
represent it---is a mapping from operator names to
operator definitions. This mapping is done by
binding operator names to operator implementations
in an environment. We sometimes will refer to such
environments as languages from here onwards,
and any references to languages in programs
are to this kind of value. In mixed-language
interpretation, each part of the program must be
interpreted in the appropriate language. We take
the closure as a suitable unit for linguistic
atomicity (if nothing else, the syntactic
considerations would make a finer grain
cumbersome!) and so we include in each closure
the language of that closure, stored as an
environment binding operator names to the
corresponding definitions.
Such a use of environments other than the variable binding environment(s) assumes the provision by the substrate system of multiple environments [Padget And Ffitch] and environments as first-class values. The way we may acheive this is described in section 6.3.
As well as the language (environment of operators) an interpreter contains the evaluator, a procedure that glues the rest of the language implementation together. It is the evaluator that starts each step of program interpretation, by finding the operator name for the current node, looking it up in the language, and calling the result of that lookup, with the node as one of the arguments of the call. Operator definitions, in turn, use the evaluator to evaluate their sub-expressions as required.
Although unnatural for some languages (such as awk), this simple representation makes representation of many languages (perhaps most current languages) simple and concise, and I consider that it has proved its worth in practice. This is supported by the common use of Lisp as a basis for implementing other languages.
In the preceding s, we have used the term interpreters as a general term for what, from here on, we call evaluators, and what we had called the standard interpreter is now called the standard evaluator. The evaluator-and-language model is just one specific model for constructing an interpreter, and so interpreter is the more general term. We will still use it sometimes when referring to interpreters but not specifically to evaluators.
An evaluator is a closure called with two
arguments: the evaluand that it is to process, and
the level which provides the context (environment,
language etc) for that evaluation. Since the
closures in the argument level have closed over
all the information needed to interpret the
program it contains, no other information is
needed by the evaluator. The program, arguments,
environment, language, and even the evaluator
itself are all included in the closure.
In section 7.1 we will see that this evaluation function is performed by one case of a more general level-based evaluator procedure. This is because the fundamental evaluator rôle is not the only part of a level's evaluator that must be thus changeable. The cleanest, most concise, implementation of a tower level evaluator turns out to be that in which each level has a general evaluator rather than an evaluator just for closures.
Reflective tower evaluation adds some new requirements to the conventional closure operation, since more information is now available in the current state of a program. To hold the extra information, we add some new components to our closures. The closures we use in this system contain all the usual parts of a closure:
and also two new parts:
language in which the procedure is to be
understood. This is an environment (see
section 3.1) binding operator
names (see section 2.3) to the
implementations of each operator
evaluator with which to process the
procedure
The implementation of an operator is a procedure which interprets occurrences of that operator when applied to a level containing that operator as the operator of its continuation expression. The mechanism performing this application is explained in detail in standprocchap. The operator definition procedure is itself represented as a closure, and hence starts a new tower. Like an evaluator closure, an operator closure takes as its first argument the level containing the closure on which it is to operate, and
This organization of the interpreter into evaluator and language brings several benefits:
This leads to a very simple standard evaluator, with a clean structure to it, that is flexible for implementation of a variety of languages (as discussed in section 5.2), and that makes it easy to modify and extend languages through reflection.
It also means that the same evaluator, being a
parameterized interpreter, may be used to
interpret programs in a variety of languages by
providing the appropriate operator definitions.
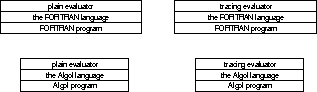
Here, for example, are some possible combinations.
Note that the language must match the
program---that is, it must provide all the
operators that the program uses---whilst either
evaluator may used with either language and
program.
Also, different evaluators may be used with the same language, calculating the same results in a different manner. For example, a level could be evaluated strictly or lazily, with or without tracing or single-step and so on. All this can be done without altering or needing to understand the operator definitions. This is possible because the interface between evaluators and languages and operators is well-defined and fixed.
Modifying several interpreter levels allows
changes to be composed together. For example,
Facilities such as unusual evaluation orders and
traced evaluation may be combined by adding
independently several special evaluators. For
example, tracing of a lazily evaluated program may
be done by adding a tracing evaluator next to the
program, and a lazy-evaluation evaluator next to
that. Were the two added evaluators to be the
other way around, the effect would be to trace how
the lazy-evaluation works; thus, combination of
tower levels is non-commutative. Such a change in
the processing of one level may affect all lower
levels. For example, it is impossible for a level
to do strict evaluation if a level anywhere above
it interprets its subject lazily. This is an
example of a property being propagated
pervasively through the
tower. Likewise, the results of adding a tracing
level will be affected by the programs of all
levels below it---this really means that the
tracedness affects all the lower levels, although
the visible effect will be only in the tracing
output---the semantics of the traced levels should
not be affected.
Furthermore, since each closure has its own evaluator and language, the properties can be changed per closure, so individual closures can be interpreted differently, allowing such things as tracing of specific procedures or operators.
Including the language in the closure also makes inter-language calling identical to intra-language calling. Inter-language procedure calls depend on having a common data representation between the languages. This is covered in typechap.
Defining new operators is straightforward, because the implementation of an interpreter is divided into small parts (the evaluator and operators) with a simple, clearly-defined interface between them. This interface hides decisions about the implementations of other operators and the evaluator, while providing all the information that is needed to interact with them.
An operator definition, as bound to an operator name in a language, is a closure, called in the same way as an evaluator, that is, with the level it is to evaluate as its argument. Thus, both evaluators and operators are written as ordinary procedures, taking each one argument. The argument is the closure that is to be evaluated, and has all the information needed for the evaluation closed into it, stored in a standard form. Operator and evaluator closures have no other interface to the rest of the system.
Since it is a closure, each evaluator or operator contains the definition of the language in which it is written, and contains an evaluator to evaluate it, evaluators and operators can be written in any language available on the system. A base language, containing operators shadowed by the meta-evaluator (see section 4.4) is provided and is designed to be suitable for use in evaluator and operator definitions. When interpreted by the standard evaluator, procedures written in the base language are shadowed, and so run faster than any other part of the tower. The base language is described in baselanguage. The base language operators provide basic flow control and provide for locating parts of a closure such as the argument list of the procedure being interpreted, and provide reflective and other primitive features.
A closure is an interpreter sufficient for
interpreting the level below it if it provides all
the operators needed by the evaluator of that
level. To maintain also the integrity of the
tower for reification, it must include a full set
of reflective operators. When these reflective
operators are provided in each level, code
reflected into a level can then reflect into the
next level, allowing reflective procedures to
capture and pass back reified data through any
number of tower levels:
Here, the actual action of reify has taken
place through something running in the
interpreter, but returning its result to the
interpreted program.
baselanguage has more detail about requirements for languages used by evaluators.
This closure-based structure for calling parts of interpreters simplifies writing reflective interpreter components, because all the information needed is reachable through the level passed as the argument to that part of interpreter. Also, since each level is the base of a tower by virtue of having a pointer to its evaluator, the information in the level also includes all the levels above it.
We now give some example operator definitions. They are written as procedures each taking one argument, the level which they are to evaluate.
(defun if (level)
(let ((expr (closure-continuation-expression
(level-continuation-closure level))))
(if (eval (substitute-expression level (second expr)))
(eval (substitute-expression level (third closure)))
(eval (substitute-expression level (fourth closure))))))
(defun + (level)
(reduce #'+
(map 'list
#'(lambda (x) (eval
(substitute-expression
(level-continuation-closure
level) x))))))
Although each individual level is simple, the
overall structure of the system is complicated.
Not only is each level the base of a tower which
stretches through and beyond the evaluator, but it
also has in the language an environment of
closures, each of which also starts a tower.
In fact, the structure is more complex than this, as each level of each of those side towers will start a new side tower from each of its operator definition closures, and so will each of those in turn---so as well as having infinitely many levels, a tower built on this basis has a number of branches---or new towers---coming into existence at each level. As can be seen in the text and diagrams of section 4.5, and as shown again in section 10.1, all of these are connected with the meta-evaluator just as the main tower is (and all those which are ever used must be grounded---as the details, presented later, of the meta-evaluator will show, in practice they all have the same meta-evaluator).
It is through the grounding of all these side towers that the whole
tower is evaluable, and so we can see that
all of these towers must use the standard
interpreter at some stage. Since the retreating
shadow technique described earlier (see
section 4.4) is used when
needed, the towers do not need to rejoin into a
single tower at the standard interpreter.
Instead, as the standard interpreter is infinitely
far away from each level, all the towers go off to
the same infinity, in parallel lines.
The meta-evaluator arranges that these parallel lines do meet at infinity, or at least just past the horizon. This is a good way to think of the meta-evaluator. Although it makes the lines meet at infinity it also makes sure that that infinity is just a little further than the furthest away that we can see or touch without moving from our present position. Although the diagram here shows all these towers as being of the same length and form, their lengths cannot really be compared (all being infinite) and their forms may vary as long as they are all grounded.
Remember also that the meta-evaluator is alongside all these
towers, rather than just meeting them at their infinitely far far
ends. One might perhaps choose to regard the meta-evaluator as
the paper on which the towers are drawn.
There is the multi-dimensional form of reflection, mentioned in section 4.5, in which a program can access its tower's meta-evaluator as the base of another tower, perpendicular to the first tower. This is useful for thinking about the implementation of the first tower, because it connects the tower to the tower's implementation in much the same way that tower reflection connects a closure to the implementation of its interpretation. Also, each of these grounded parallel towers described above meets its meta-evaluator (meta-tower) at all points along its length.
To include the meta-evaluator in the system, we
must give up the first tower's pretence that there
is no meta-evaluator, and provide a means for
going from one tower to the next. This can be
done in defining a type for towers, by making the
type connect a tower with its
meta-evaluator/orthogonal tower, and allowing any
program to find the larger tower of which it is
part, as described in
section 4.5.
Since these links lead to the next meta-level, access to further dimensions of the spiral of towers can be made possible if that is provided in the type of data used to represent towers.
This model for interpretation and interpreters brings in several new possibilities.
An unusual feature of this model of execution is the flexibility of its variable storage. The values list may be used as an open stack for stack languages, or used as though a framed stack for languages with stack frames. Using it for procedure arguments and results )as well as for the procedure's local workspace) is done in such a way that the arguments and results for a callee procedure in one language are handled correctly by the caller whatever the caller's language---even when the call goes between framed- and open-stack languages.
The environment variables are suitable for most procedural and functional languages, and are also usable by deductive languages such as Prolog to hold their bindings (instantiations) in. When a procedure in a deductive language calls one in a functional or procedural language, instantiations made by the former are visible as ordinary variable bindings to the latter. Likewise, a deductive procedure called from a non-deductive one will see as instantiations any non-local variable bindings that the latter (and its callers) may have made.
As well as being a reflective system, our system is a mixed-language one, making reified languages into part of the evaluation data that is available for manipulation by application programs running on the system.
To make the language a variable part of the context of a closure, we divide the interpreter into two parts, the evaluator, which is language-independent, and the language.
To do this, we need an abstraction for languages.
The abstraction must be general enough to handle
most languages reasonably well, and to handle all
languages to some extent. Such an abstraction can
be devised only in conjunction with an abstraction
for the programs in the languages. For the
programs, we choose to use parse trees, with each
node being identified by its operator such
as if or +, and for the languages, we
use environments binding operator names to
operator definitions.
This abstraction makes it easy to add new operators to a language, and also keeps separate the general evaluator, thus making it possible to redefine the evaluator independently from the language.
By making the language (the environment
binding operator names to operators) of each tower
level an explicit part of that level, we extend
tower reflection from being a tool for reasoning
about interpretation of programs to also being one
for reasoning about languages and their
interpretation.
``When I use a word,'' Humpty Dumpty said, in rather a scornful tone, ``it means just what I choose it to mean---neither more nor less.''
Alice Through the Looking Glass, Chapter 6