
The design of programming systems has traditionally been divided into two parts: the program being executed, and the evaluator executing it. The techniques for designing and implementing each have been kept largely separate, although they have much in common, particularly when the evaluator is itself a program (an interpreter). This work aims to bring them together, allowing the techniques of both to be used in each, by adding some special facilities to an interpreter. My thesis is that these facilities may be added, and this without unreasonable overhead in program execution time. Since this field is connected largely with program and language development work, this means that the overhead must be reasonable in the context of a large-scale prototyping system, a factor of ten being chosen as a reasonable limit. A program or language developed on such a system can then be delivered on one in which these facilities are either attenuated or removed altogether, thus bringing the speed of execution up to that of a comparable conventional system. In researching this thesis, I developed several versions of a language implementation framework Platypus, which have tended to support this thesis.
In the terms used here, a programming language (or just language) is a collection of operators, with definitions of what each operator means, and rules relating the different operators. An operator, in this sense, is the part of an expression or statement that determines what the rest of the statement means---that is, how the expression is to be interpreted. It is a token or symbol value, which is distinct from other such symbols, but, in itself, carries no further meaning. To have meaning, an operator symbol must be taken in the context of its language.
A program is a specification of some actions or functions, written in a programming language. Each function has a name and a body or expression. The language defines the meaning of the program by defining the meaning of each expression of the program and the way the parts are connected.
An interpreter uses the meaning inside the program to cause actions which are outside the program but inside the interpreter. The interpreter then causes action in the computer's peripherals to produce an effect that has meaning to an observer outside the computer. Thus, the meaning of the program is extracted from its representation in the program, and hence mapped into a different representation in a different domain.
An interpreter for a language puts these actions to work, using the rules to find its way from one operator to another. It is an active definition of the meaning of each operator and of the structure of the language.
Without a language, the program is without meaning. The program by itself is just an abstract formula in a free algebra, [Martin Löf] which does not express anything. To have meaning, it must be understood in the context of a particular language. To clarify this, consider this sentence. Without English, it would make no sense.
Taken with a language, the program can be manipulated between equivalent forms, but expresses nothing. Such manipulations are similar to reading a sentence in a natural language while writing out definitions of each word found from a dictionary and using structure descriptions in a grammar book; this performance does not need any interpretation of the sentence in any language. The program by itself is purely a data value of a type specified by the language.
But a language also can be regarded as a value in a free algebra, which can be manipulated, and applied to programs (or have programs applied to it). Continuing the analogy with natural languages, it is like a a combined dictionary and grammar book: it can be used to transform sentences, without understanding the language.
Neither the program nor the language have any further meaning unless handled by an active processing agent that makes it do something in the structural field [Smith 82] of that agent, that is, the world of things that the agent knows about and manipulates. We call such an agent an evaluator. The evaluator might be the circuitry and microcode of a computer, or perhaps it might be another interpreter. The evaluator, which is a concrete representation of an abstract language, gives meaning to the program, and in turn the program gives meaning to its input data, that is, makes results from them. The language is given its meaning by the evaluator, which is part of the interpreter---an interpreter is a combination of language and evaluator. This gives us
where the evaluator provides the meaning, which, in the traditional understanding of computation, it conjures up from nowhere in particular. In this thesis, we examine the way in which each part of a computation involving evaluator, language and program gives meaning to the other parts, and the way in which a meaning can be given to the outermost evaluator so that the evaluator can then give meaning to the rest.
To clarify this, consider this sentence. With no-one to read it, it means nothing to anyone.
Later in this thesis we refer frequently to languages, interpreters and evaluators, and it is important to distinguish between them. As we use the terms here, a language is analogous to a combination of grammar book and dictionary, as described above. An evaluator is an active agent, capable of doing something with a language and a program. An interpreter is an evaluator equipped with a language, which is then capable of doing things with expressions in that language.
In order to compute about computation, we must be able to represent information about computation, in a form which can be manipulated by a program. One such form, that has been used extensively in research on computation, is the partial program, which is evaluated through partial evaluation or reduction. Partial evaluation of a program proceeds as far as possible with the parameters available, leaving a partial program which will accept the other parameters giving another partial program. The object that remains once all parameters have been accepted and substituted is the result of the evaluation.
For example, the partial program
when partially evaluated with just one argument, produces a partial program which adds that first value to a value that it accepts as its only argument:ab.(a+b)
(which when applied to a second argument produces the resultab.(a+b))2

b.(2+b)
(b.(2+b))3
2+3
5
Application of interpreters to programs, and in turn of computers to interpreters, is described in an abstract form in the Futamura projections [Futamura 71] and implemented in the Mix system [Jones, Sestoft and Søndergaard 87]. These projections use partial programs throughout, and describe how an interpreter may be mixed with a partial program to specialize the program further, thereby compiling it. Partial evaluation for Scheme is described in [Shivers 88].
In Mix, the partial program representation is based on Lisp and on the lambda calculus. An interpreter is simply a function, as is the program, and the two are brought together by an external mechanism, the partial evaluator (or Mixer). In this thesis, the structure of a program, and that of the interpreter, are again similar, but we add a mechanism which links each program to its interpreter, and defines the relationship between them. This is a formal description of the connection between a program and its interpreter, and enables us to reason about the abstraction of interpretation and to compute with its representation, which is not possible in non-reflective systems.
In this thesis, we examine ways of including the evaluator (which could be a computer, or an program running on a computer) within our system for describing the meaning of things. This enriches our ability for giving meaning to computational processes and values, and allows us to manipulate those meanings both formally, for reasoning about them, and computationally, for handling their representations as program-as-data.
Let us now look at some properties of the components of a system that computes. In listing these properties, we will call the specification of what something does its algorithm. In functional programming, the same specification would be called a function definition. We take algorithm to be the more general term, and to embrace functional definitions. Proponents of algorithmic languages do not consider a language not to be algorithmic if it allows function definitions; whereas proponents of functional languages deem a language not to be truly functional if it allows algorithmic definitions. It is in deference to this that I have treated algorithm as a more general term than function---the two are both fully general.
The above two items are the full defining properties of an evaluator. We can also see the following properties of programs:
and from these properties, we can extend the formula on here into a more regular structure, in that neither is the program any longer a singular piece at one end of the formula, nor is the evaluator a singularity at the other end:
In this formula, the evaluator in one system is
equivalent to the program of a second system. The
evaluator of the second system is in turn a
program running in another system, and so
While much has been written about the theory and practice of program design and about the design[2] and implementation of languages, little has been done to link theory and practice with a theoretically sound and soundly practical bridge. The ideas of structured and functional programming reach out across this gap, but cannot address the link between programming in a language to the programming of the language---that is, its implementation. They can only address issues concerning one realm of programming---either the program in a given language, or the program in some language, that incidentally implements a language (either the same one or another one). The latter is the programming of a language.
To address this gap a way is needed to apply developments in the technology of software implementation to language implementation. Such a way may be found through defining language interpretation as a programmed process, with a definite model for how an interpretation is computed. With this new model, language implementation is now described as a specific form of programming, with a formal connection between the problem domain and the program domain.
Some possible reduction in execution speed, mentioned at the start of this , might come from making interpreters conform to this model rather than taking an arbitrary form. One of the aims of this thesis is to find how efficient interpreters in this model may be, compared with traditional interpreters.
A pair of techniques called reification and
reflection, not found in most computing
systems, begin to build a bridge between languages
and the programs which are written in them. They
build this bridge by describing the domains of the
elements and rules from which the language is
built, in terms of the domains of values which can
be handled by the program, and allowing the
program access to itself and to its interpreter in
these terms. Use of such access for inspection is
called reification, and for modification is
called reflection. For example, a language
which allows a program to store a stack frame for
use as part of the target of an interprocedural
jump (such as
longjump in BCPL and C) provides a
reifier for stack frames. The reflector for stack frames is part of the actual
jumping operation.
Reification and reflection are complementary actions. In some of the existing literature, the term reflection is used for them both. Likewise, a system architecture providing them may be known either as a reified architecture or as a reflective architecture. In this thesis, we use the two terms mainly in their proper rôles. When a general term for both together is needed, we use reflection.
An operator that returns part or all of the state
and code of the system is called a reifier,
and one that sets it from its argument is called a
reflector. Reifiers and reflectors that
operate on the whole state we call grand
reifiers and reflectors. Those that operator by
evaluating a piece of code in a new context, in
which reification or reflection has been done
which leaving the original context unchanged, are
called pushy reifiers and reflectors, as
they push a new context to reify or to reflect
(like a procedure call pushing a return address)
whereas those that return or set things in the
current state are called jumpy (like a
GOTO jumping without saving any return address).
(The terms jumpy and pushy come from
[Danvy and Malmkjær 88].)
We will use the term program text or just text, or code, for the representation of a program. The actual representation of the program is immaterial. The text is certainly not necessarily stored as actual text. In practice, we store it as a parse tree. This way, all considerations of the concrete syntax of a language are removed from the discussion (see section 2.4), and we can concentrate on the more abstract aspects of the language.
The state of execution of a computation---the combined contents of all its variables, along with the current point of execution and the stack of saved execution points at procedure calls---we refer to as the state of the program.
An extensional definition of an operator is given in terms of absolute meaning---what the operator is meant to do---whereas an intensional definition is in terms of how it works. In tower reflection, this distinction coincides closely with the distinction between operators used to implement a tower from outside, and operators inside that tower.
The closure of a procedure is a value that represents the text of that procedure along with any data that it requires, that is, with the bindings of any variables that it accesses but does not define. We say that the text and variables are closed over by the closure.
For use in mixed-language interpretation, we extend the closure to contain also the language and a means for applying the language to the rest of the closure. This we call an interpretive closure, but we will often simply refer to it as a closure. For consistency, we close the rest of the state into it, too.
Referential Transparency is the property of a language by which an expression may be made into a separate (named) function, and then a reference to that function (by name) used transparently anywhere where the original expression was used. It is important for abstraction.
Procedures here may return results. Like Scheme [Rees and Clinger 86], we call functions (in the computational sense) procedures, keeping functions for mathematical functions. Here the extensional equivalent of any given procedure is a function. Procedures are, implicitly, intensional.
We use a notation similar to that used for reduction in [Barendregt]. We write ``x interprets y'' as
xand ``im interprets am in n steps of computation'' asy
imWe write ``y is accessible (visible, reifiable) to x'' or ``x looks at y'' (these are equivalent) asam
xwhich reads in words as ``x looks at y''.y
Where we use two distinct symbols for equality in
describing values, we use `a b' to mean `a
and b are (structurally) equivalent values'
(
b' to mean `a
and b are (structurally) equivalent values'
(equal in Lisp terminology), and `a = b'
to mean `a and b
are the same value'
(eq in Lisp).
A reflective system, although it may appear to make the evaluator on which it runs into a manipulable data value, must eventually be executed by an evaluator running on a conventional language system. We call this the substrate evaluator, and the language in which it is implemented, the substrate language.
A program is a value in the domain handled by the interpreter. When a program is run by an interpreter that provides reflection, the program has access to its own text and state, because reflection can provide access to all the information that the interpreter handles.
In the following diagrams, the boxes represent levels of towers, and the arrows represent the flow of information between tower levels.
The simplest form of reflection is portrayed like this:
The interpreter has access to the information that represents the application (lower arrow) and the application has access to the information representing the interpreter (upper arrow). The application can get information about itself via the pair of arrows (drawn with a u-turn just inside the interpreter). Therefore,
as well asprogram0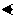
interpreter0,
.interpreter0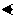
program0
In this simple form of reflection, this access goes no further (see section 2.6). In the form of reflection investigated in this thesis, called tower reflection, the program is also given access to its interpreter's text and state, as well as the program's own text and state. This is in the same terms as access to the program itself, since the interpreter is also a program:
Here,
prog0
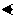
int0,
int0 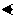
prog0, prog1 =
int0, and prog1 
int1, and int1 
prog1.
This access is modelled by including the program's interpreter in the representation of the program, like this (we are drawing these diagrams with just single arrows from now onwards, for clearer overall diagrams):
Since the interpreter is a program in the same form as the interpreted program, and the interpreter of any program may be found from the value representing the program, an infinite tower of interpreters appears, with information being passed up and down the tower in stages:
Here, for example, the program (prog0) can get information about its interpreter (int0) by asking it to ask its interpreter (int1); int1 sees int0 in the context of being prog1, so the operations required are just the same as in the flat reflection described above.
This thesis explores tower reflection, in which programming languages and the components of their implementation are first-class values that programs can inspect, manipulate and construct.
In a conventional interpretive computing system, two programs are running at once: the application, which is commonly referred to as the program, and often thought of as the only program active in the system, and the interpreter, which may be a program or the circuitry and microcode of a computer.
The sense in which both programs are running at once is quite different from concurrency. Each step taken by the computer advances the state of both programs, by the same action, in different ways. One action of the computer has different meanings at the two different levels. Also, a single step at the application level is the same piece of work as many steps at the level interpreting it. A familiar analogy to this is found in the action of a digital clock. At 8 seconds past midnight, one tick will change the seconds digit, but nothing else. The next tick will change that digit again, and also change the tens of seconds digit. Many ticks later, a single tick will advance both of those, from 5 and 9 to 0 and 0. It will also have a third effect, of advancing the minutes by 1. Many more ticks later, the tens of minutes will change... and after still more identical ticks, one more tick--- itself just the same as all the others---will have at least seven distinct meanings, including ``a new second has begun'' and ``a new day has begun''. However, the days are composed of the seconds (and so decomposable back into seconds), rather than running parallel to the seconds.
Another very relevant point in this analogy is that there are causal relationships between the adjacent digit devices of the clock. ``Tens of seconds'' changes only when told to by ``Seconds''. In turn it tells ``Minutes'' to advance at the proper time.
The metaphysical aspect, regarded by many authors, including myself, as necessary in work on reflection, in the clock analogy is that the progression of the digits of the clock does not cause time to advance. Time (an abstract thing) advances independently of the clock (a concrete thing). The activity of the clock merely models the progression of time. It does this because we choose to see the clock as representing the time. The same basic mechanism, with little modification, could be used to model or represent many other monotonous processes, such as the progress of a vehicle along the road. Likewise, an interpreter is only interpreting something, and an evaluator evaluating something, because we see it that way. Although this may seem like a frivolous aside, it is an important part of the background to reflective computation, particularly to the underlying type theory, which, in describing how a is represented by b also implies---through the action of an understanding agent---that b means a. By understanding agent, we mean something that takes in meaning (or projects meaning onto something), such as a person watching a screen. No meaning can be given to any of the system if no outside agent projects a meaning onto it in the terms of its own understanding. This is part of the symbol grounding problem---the ultimate need for a frame of reference that we can take as absolute[3].
This need for an external agent to project meaning onto something which can then be seen as an agent (but only in the light of that projected meaning) is examined in more depth and more breadth in section 4.5. There, and further on in the thesis, it is shown that the process of projecting meaning onto a process must itself have meaning projected onto it; and also that several apparently different forms of the process of projecting meaning onto processes are shown to be equivalent in both their intensional and extensional expressions. These parts of the study combine to reflect on the meaning of meaning in the context of a system that contains causal self-reference, and place that context inside the context of a system which is observed from the outside. The projection of meanings within the system, in turn, may be taken to reflect on the inclusion of that external observer as part of the system. What matters is neither the number of levels nor the dimensional complexity of the relationships between them, but the difference between looking inward into the system and outward from within the system. Looking inward, we can construct a system and move our attention into it, but looking outward cannot move attention to anything beyond the boundary of the system.
The interpreter handles the text and state of the application as data values. The text is some representation of the program code, and the state is the variables, point of execution, and the stack. From the interpreter writer's point of view, an application program is a collection of data objects---for example, the text of the program might be stored as a parse tree, the variables in a hash table and the stack as a vector, each in a variable of the interpreter---or possibly all in one variable of a suitable structure (record) type.
From the application writer's viewpoint a
conventional language implementation is largely a
black box providing little scope for adjustment
apart from the extension techniques already
mentioned. Although the application program may
occasionally handle values passed to it by the
interpreter
For computing about language interpretation, we need to make languages available in the form of data, as well as presenting programs and their state as data. Central to this thesis is the development of a suitable representation for programs in languages, the interpretive closure. In the interpretive closure, the semantics of the language are defined in two parts: the evaluator, which drives the interpretation, and the language, which defines all the operators used by the language. Reflective operators are used in both parts of the language definition.
The evaluator of the system is a program, and we represent it in the same way as any other program, that is, as an interpretive closure. The closure representing the evaluator, in turn, contains a field for its own evaluator.
This thesis is concerned with manipulating programs dynamically in the form in which they run. Transformation from input text to this form is considered static, and is not addressed here. We are not concerned here with the textual representation of the program or its data---we assume it has already been transformed from its external representation into a form in which it can be handled readily by an interpreter. Techniques for this are already well-established: for example, YACC [Johnson78] and Lex [Lesk and Schmidt 75] have been in regular use for a considerable time now, and much experience of programming them has accumulated. These and other such tools are regularly used to construct language systems for practical use, rather than on an experimental scale. Some languages allow new syntax to be established dynamically, for example by the read table and reader macros in many dialects of Lisp [Steele 84][section 22.1.5]. This is a form of reflection (a Lisp program can modify the behaviour of the Lisp reader) but it is not reflective interpretation. It may be taken further by allowing a language to extend its syntax in other ways [Köhlbecker 86] [Köhlbecker and Wand 87].
Another form of static manipulation of programs is macro expansion which is a transformation on program source [Köhlbecker et al 86]. Like syntax description, it is an important part of programming language technology, and can make use of reflection, but is outside the scope of this thesis. It can be used together with the developments described here to provide complete language implementations on a regular framework.
Before reflection was developed as a technique in its own right, it appeared in small ways in many languages, either to provide specific features or to make the language more flexible. The languages that happen to provide reflection informally tend to be straightforward and of uncluttered design, with a clear model for program interpretation, a good example being FORTH [Loeliger 81], a simple stack-based language that allows the introduction of new operators and new syntax.
In some languages there is no clear distinction between the functions that are part of the interpreter and those that are part of the application. Examples of these open languages, sometimes described as ball of mud languages, include FORTH, POP, and many dialects of Lisp [Steele 84]. They are noted for the ease with which other languages can be implemented using them as a base.
There are two ways in which such languages can do reflection:
Both of these techniques allow application programs access to the internals of the interpreter, and so perform reflection by accessing both variables of the interpreter and variables of the application program.
These languages provide an informal form of reflection and reification through making their interpreter architectures open enough to move things in and out of them. Although typically they provide little systematic support for handling programs as data, they are flexible, and provide ready interchange between the parts of the system that are manipulated and those that manipulate other parts. These language facilities have helped to show the usefulness of reflective language features.
In an explicitly reflective system, the relationship between application and interpreter is clearly defined and symmetrical. The application program can inspect and modify the internals of the system just as the interpreter can. This access is provided by the language implementation, which includes in the language the necessary facilities:
This allows an application program to add features to the language or to alter the way programs are executed. A consequence is that an application program can build a new language interpreter on a plain language base, installing each new feature in turn by reflecting it into the interpreter. Used in conjunction with syntax descriptions for parser generation, this provides a way to add a language or language features to a system, as an ordinary program rather than as a special modification to the system. Thus language and interpreter design and implementation slough off their black box status and take on the mantle of conventional programming techniques.
Through these facilities, programs have access to the computational model of their language implementation. To make proper use of this, the language should also have operations on the data types used by the model to represent interpretation, such as the insertion of new features into an interpreter, and the composition of two interpreters to provide the special facilities of both---such as tracing from one and lazy evaluation from another.
Reflective actions are also useful in the ordinary functioning of programming languages. Many languages have operations which implicitly perform a limited form of reification or reflection. For example, there may be an operation for remembering a particular point in the program as it is executed, and reverting to it dynamically from anywhere within the dynamic extent of that point in the program (that is, until the procedure containing that point has been returned from). In C [ANSI C][Section 4.6] the reifier for this is
which stores that point of execution in the variableplace: jmpbuf = setjmp ();
jmpbuf. The point is stored as a structure
containing the address in the program of {\tt
place} and the end address of the stack at that
time. This reified value can then be passed around
by the application, and eventually reflected back
into the execution state, causing execution to
continue at place again, by
longjmp(jmpbuf);
C provides simple handling of functions as values, by allowing
pointers to functions to be stored in variables. This provides a
static form of access to the program. Another reifier found in C is
the stdarg system (or vararg in some
versions) [ANSI C][section
4.8], in which successive arguments to the current procedure
call, which are components of the execution state, are extracted for
use in application expressions. The program can start reading its
arguments using va_start(pvar); and then read successive
arguments using f = va_arg(pvar, type); and finish
reading them by va_end(pvar);. In vararg,
the C program is using a library to handle parts of the C system, just
as it might use libraries to handle, for example, graphical output.
Another example of a way in which an application program could use reflection is the dynamic installation of tracing facilities in the interpreter to show the user what the program is doing. This is done without modifying the parts of the program under inspection. Likewise, an application can change its own evaluation from applicative order to normal order without modifying the program. The system described here is capable of considerably more radical reflective operations, including doing either of the above with modifying neither the program nor the language.
All features of a programming language interpreter may be programmed reflectively. In a reflective system, the code which implements any language feature used by a program may as well be in that program as in the language implementation. Taking this a step further, we can arrange for a program to implement a language. Initially, the program must run in another language, but as it installs parts of the new language, it can begin to use those parts. (Requirements for the minimal initial language are explored, as the ``Tiling Game'', in [Smith and des Rivières 84b].) This is a straightforward and natural way to define a language.
As mentioned in section 2.2, There are two main forms of reflection: flat reflection, in which the application has access to its own code and state; and tower reflection, in which it also has access to its interpreter's code and state, and its interpreter's interpreter's code and state, and so on. Flat reflection is sufficient for such operations as the non-local jump described in section 2.5, but it does not provide the facility to inspect and modify language features.
It is possible to provide a program with some access to its own interpreter without using a tower [Wand and Friedman]---that is, to just one interpreter, which runs conventionally---but this is not a regular structure and does little to model how an interpreter works. The weakness in this results from the lack of a consistent model for interpretation, that is, from its interpreter being an ad-hoc program rather than having the regular structure that is imposed by a tower of levels. In terms of our earlier analogy of the digits of a digital clock (in section 2.3), it explains the hours in terms of the minutes alone, but does not make the conceptual jump of generalization necessary to explain that hours are related to minutes as minutes are to seconds, and so cannot capture the principle behind such a clock.
Thus, flat reflective systems are suitable for implementing reflection, but not for explaining it in all its splendour.
Because the action of the interpreter causes action in the application program, when the application changes part of the state of the interpreter, it causes a change in its own state or behaviour. Through this causality, these reflective operations provide, in this example, a simple label and jump facility. This is not unusual: what is unusual is its provision through an abstract model of how a program is interpreted. Through the reifier and reflector functions the application program can add a jump facility to the language itself that was not initially present in the language. This cannot be done with non-reflective languages.
The reifiers and reflectors of a simple reflective system provide means for a program to access its own text and state. This is not sufficient for work on a reflective tower. To access anything beyond the program itself, the program must also have access to its interpreter's text and state, which can be done as already shown in the diagrams of section 2.2.
As with flat reflection, the data must be handled by the interpreter on behalf of the application---but how is the interpreter to handle this data? This data is part of the interpreter, not part of the program it interprets, and so the interpreter cannot provide it in the same way that it provides data on the application that it is evaluating. The explanation of how this facet of the tower works depends on the continuing repetitive nature of the tower itself, and the ability to pass data from level to level to level, as detailed below.
A solution to this is to model the interpreter as the application run by another interpreter, using reification and reflection provided by the second interpreter to access the text and state of the first interpreter on its behalf. (This is shown in the diagrams in section 2.2) In turn, the second interpreter needs a third interpreter to obtain access to itself, and so forth. Hence, an infinite tower of levels of interpretation appears, in which access to each interpreter is provided by the interpreter that implements it---that is to say, the one above it.[1]
There are infinitely many levels in the tower, each of which runs an evaluator. This series is infinite because each evaluator must be run by another evaluator. Using this model, we conceal any mechanism outside the tower (such as a real computer), and so can use the same model to explain the whole system. We call this mechanism the meta-evaluator or, for reasons explained in section 4.4, the umbrella, of the tower. [Smith 82] calls this the ultimate machine, a term which we do not use here because in our system, there is no ultimate machine---it is possible to go behind the meta-evaluator, as explained in section 4.5, which also explains the extension of these concealment techniques to handle the necessary processing outside the tower that makes the tower work.
Continuing our use of locative terms (such as above in the tower), the geometry of this concealment is that such a mechanism (the real computer) is alongside rather than above the evaluator that is above the application.
However, it must also be above the evaluator, to be in a position to interpret it---where Smith describes it as the `ultimate machine':
We resolve this by placing it both beside the tower, because tower levels only look up and down, not to the side, and infinitely far up the tower by inserting infinitely many levels between this real evaluator and the application.
A result of this is that however far along the tower the application looks through reification, it can never see this infinitely distant non-reifiable evaluator. Neither can it see it beside any level (because there is no means for looking in that direction). Thus, it is equally invisible in both directions, and so from the application's viewpoint these positions are equivalent. On the other hand, the evaluator beside the tower can see beside (or below--see in the diagram that they are perpendicular) itself, to the tower, and so can make the tower work.
Before the reflective tower was invented (or discovered), the concept of the meta-circular evaluator was used already to explain languages. A meta-circular evaluator is one written in the language that it interprets, and therefore capable of interpreting a copy of itself. As this was devised with no formal concept of reflection, it requires extensional operators (see section 2.1) for its implementation. Reflective operators can achieve the same ends as extensional operators but in the context of a consistent framework. For example, the implementation of a conditional statement by the first evaluator (let us call it e1) requires a conditional statement in e1---which requires the next evaluator e2 to implement a conditional statement, which means that e2 requires a conditional statement in its text, which must be implemented in e3 (the next evaluator) and so on. Alternatively, an extensional conditional, grounded outside this evaluator chain, may be used.
Of course, in a real implementation there must be an evaluator that provides these extensional operators. However, the real evaluator can be hidden away as it replaces exactly an infinitely recursive definition of the intensional one:
Here, a definition in the meta-evaluator is
just one procedure, whereas the definition of the
same procedure within the tower is an infinite
series of procedures.
It is possible for the finite real evaluator to replace exactly an infinite tower of evaluators because an application which terminates (that is, runs in a finite time) can only reify a finite amount of the infinite tower. Thus, the finite implementation of the tower can always instantiate enough of the infinite abstract tower to satisfy the reifying demands of any finite application. Any application which examined or processed an infinite amount of tower could not terminate anyway.
One of the keys to understanding the reflective tower model is to be found in understanding this implication of the finiteness of applications. Consideration of the abstract types involved is also very helpful in gaining this understanding. The types are described in Abstract Types, but before then we describe the overall system of which the types are part.
This thesis introduces several new ideas, and develops further some existing ones, which are also central to this work. The main points are introduced briefly below:
if, to be defined by procedures at the user
program level; an extension to this is...
Using these ideas, an implementation of a mixed-language meta-tower, called Platypus, is constructed, and shows itself to be passably efficient compared with conventional evaluator systems.
Reflective techniques are based on two facilities: reification, by which a program may examine its own code, state and interpreter; and reflection, by which it may modify any of these. The connection that reflection makes between a programs actions and its behaviour is causal in nature: modifications that a program makes to its interpreter may cause changes in the way that the program is interpreted.
Some programming languages, not normally regarded as reflective, provide a limited range of reflective operations, such as access to the parameter list of a procedure call. However, in a fully reflective program interpretation system, all the features of any programming language can be implemented through reflective programming in the program, thus removing the distinguished status from the interpreter of a language, and making it equivalent to any other program in the system.
There are two kinds of reflection: simple reflection and tower reflection. Simple reflection provides a program with access to its own code and state and interpreter. Tower reflection also provides it with access to its means of interpretation---that is, the mechanism by which a program is related to its interpreter, and thence to its interpreter's interpreter, and so forth. Tower reflection is more general, and, not having an arbitrary stop after the first level, is a more regular conceptual structure. Thus it is a more powerful tool for reasoning about intensional reflection and about interpretation.
Although tower reflection deals with infinite structures, it is possible to implement it with finite constructions. This thesis explores the infinite towers and their finite implementations, and investigates whether an interpretive programming system built this way can be made reasonably efficient, compared with conventional, non-reflective interpreters.
In this thesis, we develop a reflective tower implementation, called Platypus, and use it to demonstrate many of the points discussed.
``Oh, what fun it'll be, when they see me through the glass in here, and ca'n't get at me.''
Alice Through the Looking Glass, Chapter 1