We now look at the abstract types needed to
support interpretation in a reflective tower
system. Development of the type system for
multidimensional towers was an important step in
developing these ideas on reflective
interpretation.
Representing the abstract: concretion and extension
In section 2.7, we have looked at one
aspect of the concept `intension and extension';
we have seen it as applied to evaluation of
expressions or interpretation of procedures. We
now look at this topic in the more general sense
of representing any abstract things in a
computational (or otherwise linguistic) system.
The fundament of our mechanism for representing
things is Gödelization---representing each
word in a language by a digit in some numbering
system (the natural numbers being the common
case), and each instance of a linguistic construct
by the sequence of digits that represent each of
its components. (The technique comes from the work
of the mathematician Gödel [Gödel 31], who
used it in describability and computability
proofs.) Any way of representing something in
computer memory must be a form of Gödelization,
since whatever is represented must be represented
by a pattern of bit groups, as that is all that is
available.
In sections progasdata and
kindsofref
the ideas of program as data, language and
evaluator as data, and evaluation (an activity or
process) as data were presented. All of these are
built on forms of Gödelization, and presuppose
the facility for representing programs and
mappings as part of the application domain of a
program.
In looking at intension and extension, we saw that
a procedural representation (which is intensional)
for a process becomes a representation of a real
(grounded) process only when an evaluator built
of, or upon, an entire extensional definition of
the process of interpretation is applied to
it. (The representation of application
( -substitution is a suitable model for
application here) is the substitution of a number
encoding a formal parameter with the number
representing the actual parameter.) However, the
evaluator must also have an intensional
prescription (which is what is applied to the
evaluee) as well as an extensional definition or
implementation.
-substitution is a suitable model for
application here) is the substitution of a number
encoding a formal parameter with the number
representing the actual parameter.) However, the
evaluator must also have an intensional
prescription (which is what is applied to the
evaluee) as well as an extensional definition or
implementation.
Thus, somewhere within the system there must be a
link between the intension and the extension of
the evaluator, that allows the evaluator in turn
to realize the link between the intensional
prescription of a procedure and the extension of
it---a process performing that prescription. What
is the nature of this link? Is it extensional?
Yes, because a prescription of its function,
given an oracle [Turing 37], can be written. How
is the extension of the link projected onto the
link's intension? By another such link---and this
is part of the description of the link.
The example above, of representation of
procedures, shows the representation of one
abstract thing (a procedure) being used as a
concrete implementation by a context-provider that
already has a concrete (extensional)
implementation itself. Although most of this
thesis is concentrated on representing the
abstraction of procedural interpretation, the same
ideas apply more widely to representing abstract
things, including, naturally, concrete things
rendered representable linguistically by giving
names (abstract) to things (concrete) in a
computer (or other linguistic) system.
As already described in sections inout
and whatmatters, the link between the
encoding of something as a Gödel number and the
use of that number to mean that thing can be
supplied only by the user (reader) of the Gödel
number. Since we make the user---the supplier of
extensionality---be the shadow (extension) of a
further intensional description (Gödel number)
into which the original number is applied
(substituted), the user remains hidden: the
meaning cannot be found from the intension alone.
For example, given just the intension represented
by the word `skip', we cannot find its meaning.
Given a provider of extension that maps this word
onto something (an English dictionary, say; or
perhaps a Norwegian one; the two will map `skip'
onto quite different extensions, although the word
`skip' is spelt the same way) we can then find an
intension for this, if we choose to use the
dictionary this way. If, on the other hand, we use
the dictionary only to provide a textual
substitution, we simply provide another intension
(`small jump' in one case, `store sjøfarende
båt' in the other), which in turn either can be
understood to represent an extension, or
transformed by substitution into another
intension, such as, respectively, `små hopp'
and `large seafaring boat'.
In general, representation of the abstract
requires a scheme for representing values outside
the system by values inside it, with a mapping
being defined between each representable value
outside the system and the corresponding
representations within it.
The `system' referred to above is a level of
interpretation, to which an interpretation may be
given in two ways: the extensional interpretation
in terms of external values, as mentioned above;
and an intensional interpretation given by another
level of interpretation, to which the values in
our original level are the outside values as
referred to above. For example, the frequency of
an electrical signal may be represented as a
number of cycles per second, and that number may
be represented in digital apparatus by a
bit-pattern, which may be represented in
electronic digital apparatus by a pattern of
voltages.
In this sequence of
abstraction interpretation mappings,
we see a tower of meta-circular definition
appearing, much like the tower of interpretation.
Each type of value at one level is represented by
a value of some type at the level above, and these
types are in some way related. (There is general
review of types, the need for types, and the use
of types in representation, in [Cardelli And Wagner 85].)
interpretation mappings,
we see a tower of meta-circular definition
appearing, much like the tower of interpretation.
Each type of value at one level is represented by
a value of some type at the level above, and these
types are in some way related. (There is general
review of types, the need for types, and the use
of types in representation, in [Cardelli And Wagner 85].)
Is this tower of types also a reflective tower?
Yes, because the types used to describe a level of
types may be brought into that level, and types
may be moved up and down the tower. Meta-towers
of types, describing the mapping of types between
levels of types, may also be constructed, and
brought into the towers. This reflection is not
procedural---nothing happens in it; nor is it
prescriptive---it does not prescribe instructions
for doing something; it is representational and
descriptive.
These towers of representation, like other towers,
have their meta-levels linked by shadowing; an
intensional type tower (described in terms of its
structure, and then in terms of its structure's
structure, and so on) may be described without
infinite regression by an extensional type
(describing what the type means to an outside
observer).
Substituting description for prescription, we find
that not only are these representational towers
isomorphic to procedural towers, but also that
each procedural tower is backed by a
representational tower, which is more fundamental,
in that all procedures require representation, but
no representation requires a procedure.
There is a link between each level of the
procedural tower and the level of the type tower
that describes its types. This link, naturally,
has a type element to it and also a procedural
element: it is an environment (lookup table)
mapping types to procedures for evaluating values
of those types. This environment---the
type-evaluators---is covered in more practical
detail in section 7.3.
What lies beyond the type tower, as we bring
that into our system (that is, Gödelize
it---give it a Gödel number, or encoding)? What
represents the representation of the
representation? This is the meta-tower of the
tower of types. Using this, we can continue our
Gödelization of the abstract things underlying
procedurally directed evaluation. We can also
Gödelize this encoding itself, and yet still not
describe in full its connection with the
ground [Gödel 31], because from this intensional
viewpoint, we can never create an extensional view
or definition of the system.
In the discussion above, we have taken
Gödelization as the basis for representing
values of any type (including types). How can we
describe a tower or a meta-tower, given that each
tower in a meta-tower is infinitely long, and
there are infinitely many of them? Does this
require infinitely long Gödel numbers, or may we
roll up the boring section of the tower, and
encode this as such in the Gödelization, as is
done in computer memory as shown in
section 4.2? Does such an approach even
work in this rôle?
It is possible to bring these two approaches
together, by allowing Gödel numbers for
meta-towers to use not only the natural numbers
for their digits, but also transfinite numbers (if
the type we use to support the use of digit
strings as numbers allows such a mixed polynomial
as a number). In the first tower in the meta-tower
we label the levels as 1, 2, 3.... This is
infinitely long, and we can write, in place of an
infinite series of numbers (the boring section of
the tower) a single transfinite number (the
meta-tower shadowing the boring section of the
tower). Thus, we now refer to the whole tower as
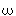 .
.
The meta-tower of this first tower has level
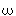 as its first level, and we label the
following evaluator levels as
as its first level, and we label the
following evaluator levels as 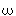 +1,
+1, 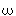 +2,
+2,
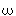 +3....
Taking this meta-tower, and writing out its
boring section in detail, we have another infinite
series of numbers, and can do the same kind of
substitution again, writing 2
+3....
Taking this meta-tower, and writing out its
boring section in detail, we have another infinite
series of numbers, and can do the same kind of
substitution again, writing 2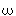 for in place
of the series
for in place
of the series 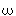 +1,
+1, 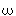 +2,
+2,
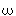 +3..., and starting a new tower, with
evaluator levels 2
+3..., and starting a new tower, with
evaluator levels 2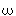 +1, 2
+1, 2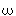 +2,
2
+2,
2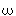 +3....
+3....
This infinite series can itself be represented as
a meta-tower (as represented by the diagrams in
section 4.5), and we label this
meta-tower as 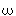 ^2, and its successive
meta-evaluator levels (drawn as gray rods in the
diagrams) are
^2, and its successive
meta-evaluator levels (drawn as gray rods in the
diagrams) are 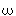 ^2+1,
^2+1,
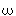 ^2+2,
^2+2,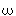 ^3+1....
^3+1....
Having explored the ideas behind the type system,
and its connection with evaluation, we now look at
what must be provided in the practical type system
that we use in implementing the tower system. As
concrete examples, we present several of the types
used by the evaluator and meta-evaluator in
Platypus.
We use a dynamic type system; a static type system
would have difficulty with interpreters being able
to pass around objects of arbitrary types for
which their subject programs have called,
particularly when the language being interpreted
provides dynamic typing. Dynamic typing being more
flexible than static typing, it also can be used
to support statically typed languages without
change.
The values in a tower reflection system may be
seen as being of two kinds:
-
the values present in any ordinary computing
system, such as numbers, characters, strings,
pointers, structures, lists and arrays
-
the values concerned with reflection, such as
closures, levels, activation stacks, expressions,
towers, value lists and environments.
To be able to perform computations on values of
either kind, we must have operations handling
values of the types concerned. Whether the values
are concerned with reflection or not is not
pertinent to how we handle them, and no types used
here are inherently reflective.
There are two groups of types that we must
consider, classified according to whether values
of that type may be divided into several parts:
-
simple types (such as numbers)
-
compound types (such as vectors and structured records)
In principle, there are two kinds of simple types
(although in practice both are usually represented
by numbers):
-
those in which the possible
values are related to each other in some
particular way, and in which a value can be
produced from other values (such as numbers);
-
those
in which values can only be created, and compared
for equality (tokens).
Since tokens can be implemented through simple use
of integers, we will not provide them separately.
(In fact, to give tokens convenient textual names,
we use keywords, as used in Common
Lisp [Steele 84][Section 11.6]. We also use the
substrate Lisp's symbols in general as tokens for
lookup in environments.)
Likewise, logical values can also be represented
as a range of integers, although their meaning is
sufficiently special that we will could them
appear as a distinct type (in fact, for
convenience, they are implemented compatibly with
Lisp, using the symbol t for true and
the empty list nil for false).
A compound type is one in which a value of that
type may be separated into elements. Each
element may be of either a simple or a compound
type. We select an element of a value of a
compound type by its index, which is of a
simple type.
There are two kinds of compound type:
-
those in which the index is a
number (vectors, arrays);
-
those in which (in this system) the index is a
token (structured records)
Since, as noted above, tokens can be implemented
as numbers, structured records can be implemented
as vectors. In this system, the vector
representation underlying a structured record is
visible, although not used as the usual route to
access the data in the record. In the Lisp
version of the meta-evaluator, records are
represented by defstructed objects in Lisp, while
in the C version of the meta-evaluator, the
array form of record is explicit, although usually
concealed through a collection of macros.
Such shifts in the nature of the same type are
covered in more detail in section 6.5.
Note that, like tokens, vectors may be compared
for equality, but not compared for order.
The above considerations give us three fundamental
types:
-
truth values
-
numbers
-
vectors
With these, we can perform all the operations of
conventional computing systems, apart from input
and output, which we assume are done for us by
operators at the next level up, which we will not
try to analyze. We must also provide support for
the types needed for reified state values. This is
done through the types that we already have, as
they are expressive enough for this.
Certain types are particularly important in the
evaluator and meta-evaluator, as they describe the
values that these procedures handle directly
themselves. The rest of this section lists and
explains these types.
The first type to describe in a list of types is,
naturally, the type for values that represent
types---that is, the type of the tags in our
dynamic type system. The main use of these is to
identify how to evaluate something. Since this may
be different in any number of different contexts
(such as different tower levels, or an evaluator
and the corresponding meta-evaluator) it is
neither appropriate nor even possible to build the
evaluation technique into the type (it is not the
same as class methods in an object-oriented
system, as they have only the one context for each
type of evaluation). Instead, we simply use the
type of an object as a key to look up in an
environment (such as a type-evaluators
environment, as mentioned later in this section and in section typeval2, and also in
sections stanproclisting
and metaevaluator). It is appropriate,
therefore, for types to be represented simply by
names. Any information describing some aspect of
the type may be found by looking that type name up
in the appropriate environment.
A closure is a structured
record, containing these elements:
The original field exists to speed
comparison in the meta-evaluator. For it to
determine whether a closure is an instantiation of
a closure that is shadowed by a kernel primitive,
the meta-evaluator looks up the original field of
the closure in the table (shadow map, an
environment) of closures that it knows to be
shadowed. The original field is copied when a
closure is copied, and changed when the closure is
changed.
The alternative to having an original field
is to compare the contents of closures to
determine whether they are the same---a
potentially time-consuming task. An idealized
implementation might do such a full comparison, in
terms of whether two closures will have the same
behaviour; however this is not necessarily
possible to determine, since it cannot even be
computed whether each of them will terminate. The
original field gives us a very quick
indication of whether the closure is still
identical to the (possibly) shadowed one from
which it was instantiated. This test is also
fail-safe; it can indicate that the closures are
different when they are still equivalent, but will
never indicate that they are equivalent when they
are not.
Closures have two rôles: when instantiated and
made part of a tower they are building-blocks for
the state of a computation. Before instantiation
they represent a stored program, and are copied
from this form into the running closures on the
stack by the procedure call mechanism, as
described in section 3.4.
Many of the data structures used in Platypus
contain many parts of the tower. In particular,
the value list of a closure (its arguments,
workspace and results) will contain whole levels
of interpretation if the closure is an evaluator.
Because of this, we print some of Platypus' data
structures in very limited ways. For example,
closures are printed like this:
#<{closure 244 (pr 1)
expr: { EVAL-IN-CL { QUOTE
{ PROGN
{ LOAD "pl-in-cl.lisp"}
{ LOAD "griss.lisp"}}}}
vals:#<[7: 20
(IF (EQUAL (LISP-VARIETY) "Platypus")
(PROGN
(LOAD "snark-interpreted.lisp"
"snark-interpreted.out")
(EVAL-IN-CL (QUOTE
(PROGN
(LOAD "pl-in-cl.lisp")
(LOAD "griss.lisp"))))))
#<File stream "griss.out">
#<File stream "griss.lisp">
NIL "griss.lisp" "griss.out"]> }>
A value list is an extensible vector of
values. When a procedure is called, the value list
contains the arguments to the procedure. The
procedure, while executing, uses it to hold local
variables. When the procedure returns, it will
have filled the value list with the results. (Like
some Lisps [Steele 84], and PostScript [PostScript 85], our
language model allows for multiple results.)
Platypus prints value lists as shown in the closure
displayed above.
The Environment Type
An environment is used to map names to
values. In this system, we use an environment
representation based on hash tables, with lists of
previous values. This is known as shallow
binding. In shallow bound systems, each symbol
(name) holds its value directly; this is suitable
only for systems with a very small number of
environments (typically one or two, as in Lisp and
other languages). Old (hidden) bindings are kept
on a list, much as for deep binding.
In other systems, environments are represented as
lists of name-value pairs, either as property
lists or association lists in Lisp
terminology; this is called deep binding. A
third possible representation, combining some of
the values of each, is described in
[Padget 84].
Another possible representation of environments is
procedural, as described in [Danvy And Malmkjær 8?], and
this appears as a possible alternative
implementation of part of Platypus in
section 7.4.
Deep binding is suitable for systems with many
environments, but searching the binding list may
be slow. Platypus uses many environments, such as
the language and type-evaluators of
each closure, and it uses them intensively (one or
two lookups for every step of interpretation at
each level concerned; see
section 7.3), so speed of lookup
is critical. We use a representation using a
hash table (as provided by Common Lisp, our
substrate implementation language; see
[Steele 84][ 16])
to hold the
current bindings (much like shallow binding, but
not storing the values actually within the symbol)
and association lists to hold the saved (hidden)
bindings.
The avoidance of building a value slot or slots
into each name (names are simply tokens, or
symbols, which may be compared only for equality)
allows us to use things other than proper names as
the names, or keys, in environment lookup
operations. This provides more
flexibility---important in a mixed-language
system, as, for example, in PostScript's
dictionaries the keys may be of any type---and
also allows more consistency between the evaluator
and the meta-evaluator, as the shadow map maps
closures to shadow-closures just as
type-evaluators and language environments map
names to closures---in effect a shadowed closure
is a name for its shadow, in the sense that the
appropriate environment (or context) is required
to find from a meaning at one level the
corresponding meaning in another level.
There are several kinds of expression. A
compound expression, often just called an
expression, is a vector of values. Each value in
it is called a sub-expression.
Sub-expressions are normally constant, although
they can by changed through reflection into the
expression. Each expression contains
-
a first sub-expression called the operator
of the expression. When the expression is taken
in the context of a closure (which it normally is)
this is a name, naming an operator closure in the
language of that closure
-
other sub-expressions, evaluated under control of
the closure named by the operator, as arguments to
the operator
References to variables are also a kind of expression,
usually appearing as not as top-level expressions but
as sub-expressions of a compound expression. Two types
are used in the implementations in this
thesis:
-
local variable names,
which are distinctly tagged integers indexing into
the value list from the extensible end;
-
variable names which represent textual names
of lexical and dynamic variables.
Other things, such as numbers and string
constants, may occur as expressions, and are all
usually treated as literal constants.
The printed form of expressions is as shown in the
expressions appearing in closures and levels and towers
in this section. Non-local variable names are
printed as textual names, and local variables in
the form #<local-2>, where the number of
the local counts from the extensible end of the
stack, such that the top of the stack is referred
to as #.
All evaluations occur in the context of a level.
Every level always has a current closure, and it
is in this that the evaluations within the level
occur; this is also where most of the context is
held. The level serves to hold the current closure
of the level and the list of those saved by
funcall operations, and also to connect the level
with the tower of which it is part, and thence to
the meta-evaluator (or meta-tower) within which
that level belongs. (The links from one level to
those above and below it, as discussed in
section 4.2, are part of the closure,
not of the level, as it is appropriate for these
to be closed into particular procedures, and thus
to be changeable by reflection to those
procedures.)
Also in the level is the template closure,
used when instantiating an inactive closure (as
described in section 3.4) into
this level.
The components of a level are as follows:
- tower: the tower of which this level
is part.
- call-record-stack: The list of saved
closures executing in this level. The front of the
list is the current closure.
- template-closure: The closure used to
fill in default fields when instantiating a
closure.
The tower field is not needed for a
one-dimensional tower, but is necessary when there
is a choice of meta-evaluators, and the
meta-evaluator for a tower is part of the
reified state of the tower.
In Platypus, a level is printed like this:
#<{Level running 244:
{ LET-LOCAL
{ NIL
{ OPENIN #<local-2>}
{ OPENOUT #<local-4>}}
{ WHILE { NOT #<local-2>}
{ LET-LOCAL { { READ-FILE #<local-2>}}
{ PRINC "in: "}
{ PRINC #<local-0>}
{ TERPRI}
{ SHOW-STATE "file loop"}
{ LET-LOCAL { { EVAL #<local-1>}}
{ PRINC "out: "}
{ PRINC #<local-0>}
{ TERPRI}
{ WRITE-FILE #<local-2> #<local-0>}
{ WHEN { EQ #<local-0> :QUIT}
{ SETQ #<local-4> T}}}}}
{ CLOSE #<local-0>}
{ CLOSE #<local-1>}}
on args}>
Just as a level holds a stack of closures, a tower
holds a string of levels, and also a link to the
meta-evaluator. This link consists of three
fields:
- meta-evaluator:
The meta-evaluator of this tower, as explained in
sections multidimensional
and metaevaluator;
- type-shadow-map:
A map from type-evaluators---procedures that
implement the evaluation of each type, as
mentioned above in the section on the closure
type---to their shadows, as described in
section 11.1.
- operator-shadow-map:
The operator shadow map, mapping operator
procedures to their shadows, also described in
section 11.1.
As well as the link to the meta-evaluator, there
is a link to the next dimension of evaluation, the
meta2-evaluator, represented as the grey rod
in the centre of the spiral in the diagram on
here, and as
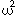 +1 in
section 6.1. (A further
mechanism, which I have not researched in detail,
is required for access to the rest of the series
that begins
+1 in
section 6.1. (A further
mechanism, which I have not researched in detail,
is required for access to the rest of the series
that begins
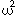 ...,
...,
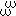 ...,
...,
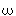
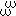 ...).
...).
A tower is a complex data structure, and
describing it in detail can take considerable
space. In practice, it turns out that the most
useful part of it to print is the program it is
running; when working with meta-towers, it may
also be useful standard evaluator (which will vary
between meta-towers). A tower is printed like
this in Platypus:
#<{tower with standard evaluator
{ LET #<<evaluation-point>>
{ { TYPE-EVAL
{ LOOKUP
{ TYPE #<local-0>}
{ LEVEL-TYPE-EVALUATORS #<local-1>}}}}
{ IF TYPE-EVAL
{ FUNCALL TYPE-EVAL #<local-0> #<local-1>}
#<local-0>}}
and program
{ LET-LOCAL #<<evaluation-point>>
{ NIL { OPENIN #<local-2>} { OPENOUT #<local-4>}}
{ WHILE { NOT #<local-2>}
{ LET-LOCAL
{ { READ-FILE #<local-2>}}
{ PRINC "in: "}
{ PRINC #<local-0>}
{ TERPRI}
{ SHOW-STATE "file loop"}
{ LET-LOCAL
{ { EVAL #<local-1>}}
{ PRINC "out: "}
{ PRINC #<local-0>}
{ TERPRI}
{ WRITE-FILE #<local-2> #<local-0>}
{ WHEN { EQ #<local-0> :QUIT}
{ SETQ #<local-4> T}}}}}
{ CLOSE #<local-0>}
{ CLOSE #<local-1>}}
}>
Note that since this tower is being evaluated at
the time, it has closures with their current
expressions being different from their procedure
expressions. The current expression is always a
sub-tree of the procedure expression. It is marked
in each of the expressions above with the marker
#<<evaluation-point>>, which is not
represented as a value in its own right; it is an
artefact of printing a closure's two expressions
together, being printed when recursive printing of
the procedure expression reaches the same point
(eq in Lisp) as the continuation expression.
The type system of a language is an important part
of the language, perhaps as important as the range
of statements available. Thus, it is important for
a mixed-language system's type system to be
flexible enough to meet closely the needs of many
different languages, while having enough
consistency of its own to allow the passing of
values compatibly between procedures written in
different languages, as well as up and down the
tower as described in
section 6.5. This is one
of the reasons why it is important for systems
such as Platypus to use dynamic typing; static
typing is simply not flexible enough to support a
system in which any level contains a dynamically
typed language.
To make the evaluator flexible enough, it is
parameterized by the
type-evaluators field of the
closures it evaluates; this contains an
environment binding type names to the closures
used to evaluate things of each type. The use of
this field is described further in
section 7.3. There is a shadow
map (see section 4.4) corresponding
to this and used by the meta-evaluator (see
section 11.1. Types not mentioned in
the type evaluator shadow map are evaluated by
interpreted procedures, so it is not necessary for
all types to be known ab initio to the
meta-evaluator---new ones may be added at any time
at any level.
Using this approach, not only do we make the evaluator
extensible to cover the addition of new types, but it
also takes on a more convenient form for reification
and reflection, as the evaluator for a particular type
may be found and replaced simply through access to the
type-evaluators environment. At an earlier stage
in the development of the evaluator, there was a Lisp
typecase statement instead of the lookup and
funcall with the type-evaluators environment; a
change in the evaluation of one type required
replacement of the whole evaluator.
Values may be passed up and down a tower. Since
the meta-evaluator does not change the
values it transfers from one level to another,
values passed between levels keep the same
intension (representation) while possibly having
different extensions (meanings). For
example, bignums may be numbers at a lower
level, and arrays of numbers at some higher level.
At the hardware level, which is the highest level,
they, like all other values, will be words and bit
patterns.
In C-Platypus, all types within the tower map onto
quite different types in the meta-evaluator: all values
map onto structures containing data words and
associated tag (type) words; booleans map onto numbers,
structures onto arrays, and so forth. This is an
example of how the type shifts between levels of a
tower are different to type shifts that go in and out
of the tower.
In Platypus89, in which the substrate language is
Common Lisp, the meta-evaluator and the tower contents
both use the type system of Lisp, and there is no shift
in the meaning of each representation (with the one
exception that string-characters are used to index
variable in the local stack frame, as they are
distinctly tagged small integers---Common Lisp does not
allow the definition of new varieties of atomic
types). The use of this is shown in
section 7.3.
In Platypus, values normally have the same
extensions at all levels of the tower, which has
removed a possible source of complexity and of
inaccuracy. All values also have the same
intension (representation) both in the form in
which a higher level uses them, and in the form in
which a lower level obtains them through reifiers.
This means that reifying and reflecting
information do not change the representation.
This is an important design point in Platypus.
Some reflective systems (such as SmallTalk-80
[Goldberg And Robson 83]) hold reifiable data in a different
form from that in which it is passed back through
reifiers. For example, a reifier for a stack
frame object in such a system might construct the
object from a real stack frame to pass it back to
the program; the real raw stack frame might be in
a unsuitable form (perhaps outside the type
system) for handling as reified data. In the
corresponding example in Platypus, the real stack
frame is passed back by the reification of a stack
frame. To make this practical, the stack frames
must be kept in a form suitable both for program
execution and for manipulation as reified data.
There are advantages and disadvantages of
translating the data between formats like this.
Among the advantages are that the reified form
might not be suited for efficient program
execution, in which case separating the
representations allows the form used by the
evaluator---the reflected form---to be designed
purely with efficient evaluation in mind; and that
levels (and other structures) that have to be
realized (as described in
sections unroll-circular-tower
and unrollmech).
Whether or not the mapping between intensions at
adjacent tower levels is the identity mapping may
be used as a way to classify level shifts into one
of two forms. Level shifts in which this mapping
is an identity are closer together than those for
which reifiers must alter the representation, as
less work needs to be done to move information
between the levels. Thus, it may be expected that
the first level shift
in each tower in a meta-tower
(see section 4.5) may well
change the representation, but others will not. At
the lower end of the meta-tower, this corresponds
to the extensional shift between the problem
domain---the external real-world meanings---and
the computational domain of manipulable values.
In general, changing the extensional meaning is
useful in implementing a tower (the representation
may change between the tower and its meta
interpreter) but is not particularly useful within
a tower, where it is more useful to pass data
between levels readily.
As levels share a type system, and can pass data
to each other, they also share a structural
field---they can share data with no need to
transform it as they pass it amongst themselves.
And yet, they also each have their own structural
fields, as the level interpreted by each
interpreter is the structural field of the level
above it and as each level can access all other
levels, the whole tower (or meta-tower) is the
structural field of each component---and this
includes that component itself.
Whatever the form of the shift between intensions
at different levels, there must be a defined
mapping to do the shifting. Without this, the
tower would be broken for purposes of reification
and reflection, and could only be used for
interpretation, imposing a one-way restriction at
one of the level shifts. This is done deliberately
in implementing the meta-evaluator in C-Platypus,
to ensure that the meta-evaluator always
remains hidden from the tower.
In making representations compatible between
levels, we also make them compatible between the
languages of each level, mentioned as a
requirement in section 5.3. This
may require some flexibility in matching the
underlying representation to each language. For
example, some languages, such as Lisp, do not have
a distinct boolean type, and others, such as
C, do not have bignums (digit string arithmetic),
and yet it might be appropriate to provide for
these in the base language and the standard
interpreter. Fortunately, the common grounds of
computability and computer architecture have
pushed language designers' intuitions toward a
reasonably consistent central set of types (such
as integer, boolean, string, array, record).
With a common type system, routines written in
different languages can pass data between
themselves without having to make any modification
or translation to the data. This keeps
inter-language calling equivalent to
intra-language calling.
The ideas behind the towers' type system are
important in understanding tower reflection. Types
are an essential part of the way we represent
values, and the mapping from one tower level to
the next is a representation of a value in one
system by a value in another. The basis for
representing values in a computer is
Gödelization, in which digits in numbers denote
words in a language.
The type system we use must allow the
representation of procedures and of procedural
evaluation, as well as the representation of the
application's problem domain. It must also be
possible to represent the infinite towers and
meta-towers used in reflective evaluation.
The system must provide operations on types
concerned with reflection (that is, types for
objects representing parts of the tower) as well
as for the types of objects normally handled by an
interpreter. We divide types into two kinds:
simple and compound.
A few types are of particular importance in a
reflective tower. Closures are the central type.
Other important types include expressions,
environments and value lists.
As information is moved between levels, its
representation may be changed, although in
Platypus it is not changed. The meaning of the
same information may be different at different
levels even when the representation is the same.
Although the meaning and representation of
information does not normally change between
levels of a normal tower, it may well have to
change in going between the tower and the
meta-evaluator that implements the tower.
The shop seemed to be full of all manner of curious
things---but the oddest part of it all was that,
whenever she looked hard at any shelf, to make out
exactly what it had on it, that particular shelf was
always quite empty, though the others round it were
crowded as full as they could hold.
``Things flow about so here!'' she said at last in a
plaintive tone, after she had spent a minute or so in
vainly pursuing a large bright thing, that looked
sometimes like a doll and sometimes like a work-box,
and was always in the shelf next above the one she was
looking at. ``And this one is the most provoking of
all---but I'll tell you what---'' she added, as a
sudden thought struck her. ``I'll follow it up to the
very top shelf of all. It'll puzzle it to go through
the ceiling, I expect!''
But even this plan failed: the ``thing'' went through
the ceiling as quietly as possible, as if it were quite
used to it.
Alice Through the Looking Glass, Chapter 5
Submitted, Examined And Accepted: 1991
Contact me
 -substitution is a suitable model for
application here) is the substitution of a number
encoding a formal parameter with the number
representing the actual parameter.) However, the
evaluator must also have an intensional
prescription (which is what is applied to the
evaluee) as well as an extensional definition or
implementation.
-substitution is a suitable model for
application here) is the substitution of a number
encoding a formal parameter with the number
representing the actual parameter.) However, the
evaluator must also have an intensional
prescription (which is what is applied to the
evaluee) as well as an extensional definition or
implementation. interpretation mappings,
we see a tower of meta-circular definition
appearing, much like the tower of interpretation.
Each type of value at one level is represented by
a value of some type at the level above, and these
types are in some way related. (There is general
review of types, the need for types, and the use
of types in representation, in
interpretation mappings,
we see a tower of meta-circular definition
appearing, much like the tower of interpretation.
Each type of value at one level is represented by
a value of some type at the level above, and these
types are in some way related. (There is general
review of types, the need for types, and the use
of types in representation, in 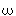 .
.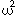 +1 in
section
+1 in
section 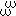 ...,
...,