Adding reflection and reification to a meta-circular evaluator can make it a more useful tool (or model) for describing the language it implements, but does not add to our ability to handle programming languages in general. We need to make the language an explicit parameter of each level of evaluation, and provide each level with access to its language. Consequently:
In making the language an explicit part of each level, and thus in letting it vary from level to level, we must ensure that there are compatible data representations throughout the system, so that values may be passed freely between languages and between levels. The requirement is not that all levels must have the same representation system, but that adjacent levels must be able to translate information from one representation to another so that they can transfer data between them. This is normally met by the reifiers and reflectors translating the data between the different representations, as discussed further in section 6.5.
The availability of data produced by reifying levels, and the consequent possibility of levels passing levels as data to each other, requires that the representation of levels also be compatible at all levels.
In order to handle parts of a computing system as data, we need a data type for representing parts of a computation. The computation is something active, and its activities may be prescribed procedurally. However, such procedural descriptions are static, and do not represent the actual computation. Computation must be represented with a combination of its (procedural) prescription and a snapshot of its state at some particular time---which part of the procedural prescription it was executing, and on what data. It is important that the representation used:
Since the components of program texts are procedures (see the note on procedures and functions in section 2.1), and the components of program states are the states of individual procedures being evaluated, we will use a type combining them, the closure of a procedure (see section 2.1) as our basic type for describing tower objects.
A closure closes over the code and state of a procedure, making procedures into self-contained values that can be passed around complete with the state that they need. For convenience, we split the state into two parts, local and non-local, so the closures used here have three components representing the state of a procedure:
expression of the closure,
which represents the text (or body) of
a procedure
value-list, which contains the arguments
when the procedure is called, private internal
state while it is being evaluated, and the results
as they are prepared to be returned to the caller;
environment, which
holds all non-local variables accessible to the
closure, bound in other closures (called
lexical or free variables).
The expression of a closure we represent as a
`parse tree' of the procedure text it
represents. Each node of the tree has as
its first sub-expression a node type (which we
call its operator) and possibly some other
sub-expressions, which are taken as
arguments to the operator. For example, a+b
has the operator + and the sub-expressions
a and b. This representation is used
for all programming languages in this system.
Although the system we build does not make this
form of expression a strict requirement, in
practice we have found no need for other
representations.
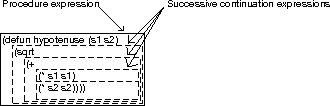
In fact there are two parts to the expression of a closure: the procedure expression and the continuation expression. The procedure expression is the whole body of the procedure, and the continuation expression is the sub-tree of the procedure that is currently being executed. (At any point, a frozen state of computation may be continued from its continuation.)
The reason for this is that we need to know at all
times both the current point of computation, and
the whole definition of the procedure. As the
continuation expression moves inward down the
expression tree, we need the procedure expression
for reifiers to find what the original procedure
was. If we were to have only one expression in
each closure, it would not be possible to return
to the evaluation of an outer expression on
finishing evaluating an inner one, except by
storing the information in the next level above in
the tower---which, although convenient for
interpretation (because it is part of the state of
that interpreter), is inappropriate for
reification, because that is not the level to
which belongs. For example, when in evaluating
(lambda (a b c) (* (+ b c) a)) the evaluator
is at (+ b c), the (* ? a) must be
stored ready to be resumed when (+ b c) has
been evaluated. It would also make it impossible
to make procedure calls (or even expression
evaluations) that do not start new instances of
the interpreter's context.
This part of the model of execution is analogous to that of compiled code in many conventional systems. Each call level has a stack frame, in which are (or may be) stored pointers to the local variables used, the environment active at that point, a pointer to the start of the procedure, and a current execution pointer for the procedure (the return address for the unreturned call it is making).
The interpreter uses the operator of the
continuation expression to choose what to do at
each step of interpreting a closure. For example,
in a+b, it might evaluate each of a
and b, sum their results, and return that
value to the surrounding expression. The operator
is all the information the interpreter needs to
decide how to select what to do at that node.
The classification of variables into two kinds formalizes the common practice in language implementation, while also providing purely positional parameter passing---that is, without needing common knowledge of variable or parameter names between caller and callee---which is necessary for referential transparency (see section 2.1).
The value list corresponds to the stack frame or activation record of common practice, and shared between call levels within an evaluation level, and the environment is equivalent to the display of languages such as Pascal.
The value list as we use it takes the form of an open stack. Each procedure may add or remove things at the end of it, and access items by indexing into the stack from the end. Before calling another procedure, a procedure making a call pushes the call arguments onto the end of the value list. The callee will then be able to use them as its arguments, and also use the same locations and any that it may add beyond them for its own local state (workspace). Before returning, it will pop its workspace and arguments, and push its results, if any, where the arguments and workspace were.
This form of stack is compatible between languages with an explicitly open stack, such as FORTH and PostScript, and those with closed stack frames, such as Lisp and Algol. With such a stack, cross-calling between these kinds of languages is automatically available.
As well as being used as a Lisp-style environment or a Pascal-style display, the environment may be used to hold unification variables for languages such as Prolog. This allows variable bindings, made by other languages, to appear as instantiations (unification bindings, or substitutions), and allows unification bindings to appear as ordinary variables when a procedure in a unification language calls one written in a non-unification language.
Here is a Lisp definition of a closure, which will be used in example code later:
(defstruct closure ;; a function to interpret the closure: (interpreter (type closure)) ;; a Lisp s-expression: procedure-expression continuation-expression ;; arguments, workspace, result: (values (type vector)) ;; an alist or hash-table: , perhaps? (environment (type lookup)))
The nature of the interpreter field of the closure is described in section 3.2. Here, we just show it as a closure, but in fact it contains several other components.
The introduction of mixed languages to a reflective architecture, and with it the idea of programming languages as values, adds a new requirement to the closure operation. As well as the procedure texts and states, closures must close over the language in which that text is to be interpreted. Commonly, a program text is written on the assumption that it is to be interpreted as a program in just one specific language, and so it is generally reasonable to say that a program is in (or for) a particular language. However, the language is just part of the context---it is the semantic, or linguistic, context---within which the program is be evaluated, and so could vary, just as the value context provided by the lexical and dynamic environments may vary. For most purposes, though, it is appropriate to close the text and the language together, so that wherever the text is seen, the associated language is made available with it. Therefore, we may say ``the language in which an expression is written''.
There are several places at which the language could be specified in representing programming systems. Attaching a language to each procedure (as part of the closure of that procedure) allows procedures at the same level of interpretation to be written in different languages, which is what is required for normal mixed-language programming as mentioned in section 1.6.
Two effects of closing the language into the procedure representation are that:
To evaluate a closure, we use the language interpreter which is a component of the closure. This interpreter is itself a procedure (stored as another closure), and takes the other parts of the interpreted closure as its arguments:
(defun eval-closure-0 (closure) (funcall ; to evaluate a closure, (closure-interpreter closure) ; call its interpreter (closure-procedure-expression closure) ; with the expression, (closure-continuation-expression closure) ; values, and (closure-values closure) ; environment (closure-environment closure))) ; as arguments
but, for orthogonality and for convenience in reification and reflection, we make it take one argument, namely the closure in which it occurs:
(defun eval-closure-1 (closure)
(funcall ; to interpret a closure, call
(closure-interpreter closure) ; its interpreter, with the
closure)) ; closure as argument
Since the interpreter of a closure is itself a procedure (represented as a closure) this evaluation goes infinitely high up the tower, and we see a tower of active closures forming, rather like a tower of meta-circular interpreters.
There is a simple set of rules describing how adjacent levels of a tower are connected, and how the rules for adjacent levels can be extended transitively to longer strings of levels.
Unlike a meta-circular interpreter ia that must always be interpreted by an interpreter ib such that (using the notation introduced in section 2.1)
(iaib)
(ia
ib)
our neighbouring interpreters are allowed to be different:
iaib
while still requiring
iaib
Each interpreter also provides means to pass
information between its own closure and the one it
interprets, (ia  ib as well as ib
ib as well as ib
 ia---the latter is always the case), so
we have a reflective tower, where each closure is
provided (by its interpreter) with access to
itself:
ia---the latter is always the case), so
we have a reflective tower, where each closure is
provided (by its interpreter) with access to
itself:
(ia  ib) ib) 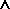
|
((ix
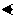 iy)
iy)
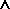 (iy
(iy
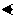 iz)
iz)
 (ix
(ix
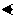 iz))
iz))
|
 (ib (ib 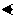 ia) ia)
|
(ib 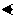 ia) ia) 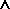
|
(ic 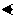 ib) ib) 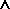
|
((ix 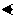 iy) iy) 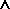 (iy
(iy 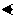 iz) iz)  (ix (ix 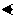 iz)) iz)) 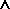
|
(ib 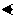 ic) ic)  (ia (ia  ib) ib)
|
Thus, the ability of a closure to receive access to itself depends on the closure's interpreter; and, in turn, that interpreter can only have access to itself if its interpreter provides reification.
Before looking at how this tower is held together, we must understand how a procedure is called using these closures. There are two ways of doing this:
In the first form of procedure call, to interpret a call of a procedure directly, the interpreter must do the following actions:
values with the arguments to
the call.
In the second form of procedure call, the interpreter may itself recurse to make the new stack frame, thereby making its interpreter hold the saved continuations, which it must do in the manner described above---or, in turn, by making the next interpreter hold the previous continuations...---and that may in turn make another interpreter hold the previous continuations, and so forth. The second method is particularly appropriate for interpreting a language where all calls are reflective, as the whole closure is always the object passed around.
However, this makes it impossible to make non-reflective calls, which is unfortunate, because reflection into a interpretation of a level no longer has the desired effect; instead, we would just reflect into the interpretation of a procedure, and the effects of the reflection would be lost when the procedure returns. So, we choose the first method for normal procedure calls. These two forms of procedure call are covered in more detail in section 8.2.
Interpretation of a procedure works by recursive descent of the procedure's expression tree. At each node of the tree, the node's operator directs the interpreter how to handle that node.
For example, an operators for flow control, such as
if, may call the interpreter explicitly to
implement that flow control, using its own flow
control to decide when to call the interpreter: so
to interpret
if a then b else c
we can use
(defun if (closure)
(let ((expr (closure-continuation-expression closure)))
(if (interpret (first expr) closure)
(interpret (second expr) closure)
(interpret (third expr) closure))))
An operator which does no flow control, which we sometimes refer to as a Lisp-like operator, as it is similar to a Lisp procedure in the way that its argument sub-expressions may be evaluated, may evaluate its sub-expressions in an arbitrary order. An example is:
(+ a b c d ...)
The simple applicative order version shown here evaluates them from
left to right, using the reduce procedure of Lisp
[Steele 84][Section 14.2],
which applies a given procedure taking two arguments to each element
of a sequence and an accumulating result:
(defun add (closure)
(reduce #'+
(map 'vector
#'(lambda (expr)
(interpret expr closure))
(tail (closure-continuation-expression closure)))))
The definition of each operator is a closure a procedure which, when applied to a closure, interprets it in the appropriate way. Operators are done this way to facilitate language definitions and mixed language working, as explained in section opprocs.
The call stack of each level is made of a sequence of closures each representing an active instance of a procedure. A program is stored as a collection of inactive closures waiting to be copied. When a procedure is called, its inactive closure is copied onto the call stack to make an active one, much as the calling mechanism of a conventional interpreter builds a stack frame for the procedure being called. Pointers are stored in the stack frame to point to the previous stack frame, to the procedure body (code), and to the static or constant data needed by the procedure; the variables provided by the procedure will also be linked into the environment.
Whenever a procedure is called non-reflectively, its closure is instantiated, the value list of the new copy filled in with the call arguments, and the closure placed on the stack of the bottom level of the tower, where it becomes the current closure. This creates a new activation record within the bottom level of the tower, but does not add a new level to the tower.
When a procedure is called reflectively, a copy of the interpreter of that procedure's closure is taken, with the closure as the interpreter's argument. The copy of the interpreter is installed just above the bottom of the tower, where it runs a new level of the tower.
Since in either form of call, the closure is placed in the tower, the tower always provides the context for evaluating the closure.
At each level in our infinite tower, there are one or more procedures, of which at any one time one will be active, and some (possibly none) will be on a list of saved procedure evaluations to be returned to.
In common with many other language systems, we represent procedures by closures, each containing the code of the procedure and any context that must be carried with that code to interpret it.
To make explicit the interpreter of a procedure, we close over the interpreter when constructing the closure of the procedure, and thence the rest of the tower of which that evaluator is the lower end, thus making it contain the whole of the context in which the procedure is interpreted.
A closure constructed this way we call an interpretive closure, since it encloses all the information needed for interpreting a procedure.
We use interpretive closures as the building block for constructing reflective interpretive towers. Each level of a tower contains a closure (actually, a stack (or list) of closures). The interpreter of an interpretive closure is also an interpretive closure, as are the operator definitions. Closures are also used to represent procedures available for calling. When a procedure is called, its closure is instantiated by copying in onto the top of the stack, and filling in fields that come from other parts of the level and the tower (such as the dynamic environment within which it was called.)
And the whole earth was of one language, and of one speech. And it came to pass, as they journeyed from the east, that they found a plain in the land of Shinar; and they dwelt there. And they said one to another, Go to, let us make brick, and burn them throughly. And they had brick for stone, and slime had they for mortar. And they said, Go to, let us build us a city and a tower, whose top may reach unto heaven; and let us make us a name, lest we be scattered abroad upon the face of the whole earth.
And the Lord came down to see the city and the tower, which the children of men builded. And the Lord said, Behold, the people is one, and they have all one language; and this they begin to do: and now nothing will be restrained from them, which they have imagined to do. Go to, let us go down, and there confound their language, that they may not understand one another's speech. So the Lord scattered them abroad from thence upon the face of all the earth: and they left off to build the city. Therefore is the name of it called Babel; because the Lord did there confound the language of all the earth; and from thence did the Lord scatter them abroad upon the face of all the earth.
Genesis 11:1-9