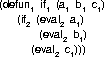Having produced a model of computation on a reflective theme, we now examine its use in modelling existing computing systems and thereby in re-implementing existing languages with the addition of reflective features and mixed-language working.
Our reflective core system is concerned mainly with program structure and control, and makes no attempt to cover such facilities as arithmetic. These must be assumed to be available at ground level. We can build on such ground level facilities, but do not attempt to describe them, instead leaving them to be described by conventional mathematical means (for arithmetic) for example. Likewise, input and output are not covered by our system, but must be made available in some form from the ground level. These facilities tend to be similar in most languages; they depend not so much on the language as on the host computer system. However, input could be seen as a form of reflection, putting into the system data from outside it, and output as a form of reification, copying data from inside the system for things outside it to use. If such communication is done with another such system, it may be seen as a form of co-tower relationship, as mentioned in section 4.5.
As well as implementing the immediately visible constructs of a language, reflective operators may implement and control the infrastructure of a language system, such as the binding of values to symbols.
We take procedure (or function) application as the most fundamental facility to describe. Like Lisp, we can claim a distant connection between our procedure (closure) application and lambda reduction.
Although, as explained in section 7.5, our procedure application does not implicitly evaluate arguments, it is in many ways similar to that of Lisp or Scheme. As well as using closures as procedures we can use them as continuations [Rees And Clinger 86] and as meta-continuations [Danvy and Malmkjær 88]. A meta-continuation is to a tower as a continuation is to a stack. It represents the frozen state of a tower, much as a continuation represents the frozen state of a process. We will use the term meta-continuation both for the continuation of a simple tower, and for that of a meta-tower of any dimensionality.
The result returned by a reifier is always either
a meta-continuation or part of one. Because
meta-continuations are values of an ordinary
structured type, programs can manipulate (or
create) them just as they do any other data; this
manipulation is not reflection, and has no effect
on the live state of the tower. Reflection
occurs when a meta-continuation is explicitly made
into the new tower state. By calling and passing
meta-continuations, co-routine-like towers
(co-towers) may be implemented. Indeed, any form
of flow control may be done by reifying, modifying
and reflecting meta-continuations, although this
is not necessarily the best or cleanest way of
implementing features; if it maps poorly onto the
implemented language's own model of computation,
it may be quite obscure, and not make it at all
easy to handle the reified data.
Reflective and non-reflective calls
There are two classes of procedure call, between which it is important to distinguish:
In this way, the tower is the call stack for reflective calls.
In implementing Lisp on such a reflective substrate, non-reflective calls can be used to implement Lisp's procedure calls, while reflective calls can be used to implement Lisp's special forms. This is covered in detail in [Smith 82] and [Smith And Des RiviÈRes 84a].
It is natural, in writing programs in the base language of such a system, to make all calls reflectively, so that each procedure called can be reified as a full tower level in its own right, with all the information being available directly. Also, intuitively this seems right; it makes the power of reflective calls available at every call, as well as organizing the arguments into a regular form, in which the argument passed is always the overall state. The callee then extracts the information it needs from agreed places in its single argument, which for a traditional call means from the top of the value list.
For the design of new languages, the distinction between reflective and non-reflective calls seems artificial, and the provision of non-reflective calls unnecessary, when reflective calls are always available. Using just the one form of call throughout makes the tower into a simpler structure than is possible with two types of call. Unfortunately, it is not possible to abandon non-reflective calling and still implement most existing languages smoothly, because their designs typically assume that everything exists at the same level; while this would not prevent our reflective model from being used for interpretation, it would make the results of reifiers be a poor match to the language's own model of computation, because extra tower levels would appear that would not map onto any level shift apparent in the source language. Since one of the aims of this development is to allow programs to extend the languages in which they are written, this is worth avoiding.
Procedure calls may done implicitly by the
standard interpreter, using the funcall
operator, if an operator definition is not found,
as explained in section 7.3.
When this happens, a level is constructed which
will run the funcall operator on the
procedure to be called. The default funcall
action (which this operator is expected to
provide) should evaluate the arguments to the
procedure, thus making the normal calling by
call-by-value. Call-by-name is nearer to the
reflective calls mentioned above, as the
information structure of the argument will not
have been collapsed down into its simplest form,
but will be in its original form, which names
the value.
If this automatic evaluation of arguments is required, it must be provided by the routines that read programs from the input files and convert them into parse trees. It is very simple to embed each procedure in the user program in a standard piece of code which calls a procedure which evaluates each element of the calling expression, putting the results onto the value list in turn, before calling the procedure body.
The procedure calling mechanism in our system is in general based on that of Lisp, while also being designed with other languages in mind. It is a fairly primitive operation: features such as choosing different procedure bodies according to the form of the argument list (useful for ML, for example) are not provided; they must be moved into the bodies of the procedures that need them. This implies that some re-arranging may be required to go from source code in such languages to our common parse-tree form of procedure bodies. While this may make the reified forms of procedures less natural in some cases, it also makes them common, so that a program in any language can understand data representing reified programs from any other language. With a suitable choice of operators, it should usually be possible to find a reasonable compromise; for example, in ML, procedure bodies might always have as their top-level operator something that chooses which part of the procedure to run, according to the arguments list, and have as the sub-expressions of that top-level expression an alternation of guard clauses and original definition bodies (a bit like Lisp's COND construct). Worse mismatches than this occur with non-deterministic languages, as covered in section 8.8.
Open-stack languages are easily accomodated, as
the design of the stack shares the local data
section between caller and callee---a little like
register windowing in CPUs such as the SPARC.
For languages which view the local data as a
stack, the top item is what other languages regard
as the first argument. This conveniently allows
procedures with a variable number of arguments to
use the earlier arguments to decide how many
arguments to use. It does, however, mean that such
things as Lisps's &rest and
&optional argument control must always be
implemented with the help of the caller, so that
the extent of the arguments to a particular call
is always known; it is not possible to say ``the
rest of them'' or ``all of them'' where a local
stack is shared without distinction between all
levels of procedure call; some form of marker must
be used.
This is a problem which requires further
investigation, as it is undesirable for a caller
to have to know whether a particular callee
requires a marker at the end of its argument list.
Probably the best solution is for the marker to be
used always, in which case the funcall
procedure and any equivalents (such as
apply) must always supply it (which is no
trouble) and all procedures must understand it in
receiving their argument lists. It is then
appropriate that they leave it there, to mark the
end of the result list---some languages, including
Common Lisp [Steele 84] and
PostScript [PostScript] allow multiple
results---for the funcall procedure to
remove when the callee has returned. Non-local
control transfers (throw, longjump)
must also be able to work with these markers.
In a language in which all calls are by value, it is not possible to implement a flow control construct using a procedure written in that language (at least, at that level of interpretation) except by quoting its arguments (in Lisp terminology)---in which case the new construct is not on a par with those initially built into the language, which require no quotation.
The few traditional language designs and implementations that have addressed this problem have used two techniques: macros, and call-by-name (fexprs, in Lisp). In both of these techniques, the body of the construct is not evaluated before being passed to the procedure, but is passed as a piece of program text. A macro transforms that text to another text, which is used in its place, while a fexpr performs directly the action denoted to it by the text.
In many languages, macros are defined in a part of the
language that is separate from the rest of the
language; the \#define construct of C is a good
example---it may even be handled by a program separate
from the C compiler.
These macro languages are unusual in having no interpretation semantics of their own---they are semantic parasites on their host languages. This separation may be taken as a form of mixed-language programming.
Lisp, however, uses its main language for macro expander functions; to tailor further its suitability for this, it has provided a feature specifically to help with this, the back-quote.
The implementation of conditional operators requires
conditional operators in the language used for the
implementation, and so conditional operators of some
kind must be present in the ground interpreter. The
ground-level conditionals may be described in
conventional terms:
(if a b c) 
(a b c ) . b
when a = true
(if a b c) ( a b c ) . c
when a = false
but the aim of our system is not to make these
attempts at absolute statements but to describe
each level in terms of another level. So instead
of the conventional description above, we use our
intensional description:
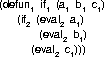
in which the fundamental conditionality is
transferred to another level, and thence
infinitely far away. Thus, it, like input, and
random numbers, is a feature that we can use, but
cannot generate. So, to use conditionality, a
closure must be linked with integrity over
conditionality to a grounded interpreter that
provides conditionality (a conditionality termed
ef (etensional if) by Smith).
Since we want the standard ground interpreter to be very simple (so that it is a minimum pinning-down to Turing-computable reality) we will make it provide only one form of the conditional:
if aand other levels and languages can build their own conditional forms from this as needed, such as Lisp'sthen belse c
cond.
Iteration, involving destructive assignment to state, is often regarded as undesirable in language descriptions, and so represented with cleaner tail-recursion. We can use tail-recursion, or we can represent it as side-effects. Since in representing it as side-effects we must use an iteration construct in the level above, we present a paradox by saying that at one level it is iteration by side effects, but at the next level it could just as well be represented indirectly by tail-recursion.
In the terms introduced in section 2.1 and described in [Danvy And Malmkjær 88] and in section 9.4, if we represent iteration as iteration, we use jumpy continuations, whereas if we make each loop into a tail-recursive procedure without converting the tail-calling to tail-jumping, we can use pushy continuations. Since a pushy continuation with tail-reflection removed is equivalent to a jumpy continuation (see section 9.4), for normal program interpretation this does not make much difference: programs will behave the same way.
In practice, converting iteration into
tail-recursion may make reflection into loop
control variables more obscure, because it
separates loop bodies into sub-procedures (
Using the grand jumpy reflector (the reifier that
returns a simple snapshot of the whole of the
current state and code---see
sections terminology
and grandjumpyref) that assigns the entire
state of the system from an arbitrary value that
an arbitrary level has produced, we can implement
any kind of flow control structure. For example, a
GOTO may be implemented by capturing the
state, changing the continuation expression of the
current closure (see section 3.1)
and making that modified state the new state. A
non-local exit may do likewise, but also take some
stack frames away entirely before changing the
expression of the current continuation closure of
the last remaining one. A reflective system
permits another form of non-local exit in which
several levels of the tower may be spanned. This
exit may carry with it, to the catcher of the
exit, information from further into the tower or
meta-tower, thus being both an exit and a reifier.
This can be used to pass back to a program errors
in the interpretation of that program.
Assignments are straightforward, since we can change any part of the state of the system through reflectors. To make an assignment to a variable, we simply write into the appropriate slot in the structure holding the current level's data. Each level's data is stored in the values-list and environments of the closure representing that level.
Local variables are referred to by indices into the value list (from the growable end of it) and non-local variables by symbols which must be looked up in the environment (which could be a hash table, for example). Binding a local variable means making a new local variable to hold values referred to by that name, while binding a non-local variable means storing its old value in a saved bindings chain associated with the environment's lookup table.
Variable access in conventional languages is often compiled in-line, and is perhaps a good example of how levels could be merged (`mixed' [Jones, Sestoft And Søndergaard 87] [Danvy 87]) to produce programs with the reflection partly compiled out---variable access, although here defined in terms of reflection, is an operation that can be done non-reflectively, and so is a candidate for compiling out on a suitable combined reflective-and-plain system, as suggested in section compilefficient.
On the whole, we have assumed that a dynamic typing system (see typechap) is available for use throughout the system, and that it is provided by the ground level, and is consistent throughout the system.
Static typing is, of course, possible; the values are still tagged as normal, but a particular language's input parser may have checked the types as it builds the parse tree which we execute.
It is, in general, desirable to keep the same type system for all levels (for ease of passing data between levels at reflection and reification) but it is possible for a level to implement special typing requirements for the level below it. which is acceptable except in first-dimension level shifts, where it makes the underlying implementation repeatedly translate data as it moves it between levels---work which is best avoided when much data must be passed between levels.
In a shift in the second dimension, that takes us to the system that implements non-reflectively the first tower, it may be commonly useful, and desirable, to change the type system to help with modelling the representation scheme used in the first tower.
The reason for this difference is in the meaning of each kind of level shift. The usefulness of changing the type system is for implementing the type system of another tower, whereas within a tower it is useful to have the same type system throughout, to make it simpler to pass data between levels.
Reification and reflection are useful in
object-oriented systems, so that an object
processing a message can invoke further methods by
sending other messages to its self (that is,
to the same object). This self-reference is a form
of reflection. In the language structure
represented here, we can model each object or
actor by a closure, which closes the programmed
actions (methods) of the object with the
environment within which it originated. When the
actor receives a message, the closure has its
expression modified to contain the message, and
is then evaluated.
Languages with parallel evaluation constructs
[Ben-Ari 82] may be implemented using our model of
interpretation, with operators that use jumpy
reflectors to switch evaluation contexts. For
example, to implement Occam's [Occam 84]
par construct, a par operator could be
written to create new contexts (threads of
execution) and put them onto the list of contexts
being executed, and the operators that rendezvous
between threads (input, the ? operator, and
output, the ! operator) would perform the
context switching required; ? would transfer
control to the thread from which the input will
come, and ! would transfer control to the
thread which will receive the output.
Our evaluation framework has not been designed with genuine parallel evaluation in mind, but it could be added in the same way that it can to any other serial execution system.
Declarative languages do not map well to the model of interpretation that we use here. One way of implementing them on it is to procedurize the programs, so that they run in a manner more like that of procedural languages [Clocksin And Mellish 81] [Warren 80].
For example, the clauses
fish(A) :- chondroicthyes(A); fish(A) :- osteoicthyes(A);procedurizes to make
(defun fishp(A)
(or (chondroicthyesp a)
(osteoicthyesp a)))
However, with the need for backtracking and cuts, the translation is more complicated than this---one approach is to use Continuation Passing Style [Haynes et al 84] [Jackson] [Abelson And Sussman 85]. Another is to write an evaluator that implements them in any convenient manner, providing suitable procedurized operators in its language---it need not use these operators for execution (it would have alternative means for doing the real evaluation), but should provide them to allow program analysis and compilation. Closures in this form should still support the protocol required for tower levels, so that they can be used as evaluators, and can be interpreted by ordinary evaluators.
There are further problems arising from the
nondeterminism commonly found in declarative
languages. It is in principle possible to match
this with the rest of the system by writing a
special version of the evaluator, which handles
collections of results (non-deterministic results)
as though they were single values, and makes some
kind of translation when transferring data in out
of this world. However, this is almost certainly
of very limited usefulness---for example, what
should the + operator do when asked to add
two such non-deterministic values (possibly with
each of them having a different number of possible
deterministic values)? A better solution is
probably to provide extensions to such languages
to improve their interface with conventional
languages, for example using streams [Steele 90]
or generators [Perdue And Waters 90] or
some other form of lazy evaluation to work through
successive possible results.
Another approach requires specialized libraries for programs that want to call across this divide---bearing in mind the specialized application that such programs are likely to have, this may well be appropriate (or at least unobtrusive) but it is not the purely transparent cross-language calling that we generally hope to provide.
One way in which Platypus does facilitate cross-calling between unification languages (a subset of declarative languages) and procedural languages is that the environment of the continuation closure may be used as the unification environment, and the value list is a suitable common form of argument/result list. When a procedure in a unification language calls one in a procedural language, the instantiated unification variables are available to the procedural procedure as normal dynamic variables, and when a procedural language procedure calls a unification one, bindings made by the procedural code appear as instantiated variables to the unification code.
As well as being useful for the implementation of
language features, reflective programming
techniques may be used to alter the implementation
as the program runs. As an example of this, I
implemented a procedure to evaluate a form using
deep binding instead of the semi-shallow binding
that Platypus normally uses. There were three
parts to this change: new implementations of the
binding and assigning operators (let and
setq in the Lisp-like base language); a new
implementation of the type evaluator for symbols
(variable names); and an adaptor function to
evaluate a form given as its argument, with
conversion of environments between the standard
representation and the new one happening before
and after the evaluation itself. Some of the code
used is presented in the following paragraphs.
Before reading this re-implementation of variable
access, it may be instructive to consider how much
effort would be involved in making the same change
to a non-reflective evaluator, or to a reflective
evaluator that does not use the evaluator,
type-evaluators and language structure
used in these experiments.
First, the new lookup and binding procedures that are reflected in. A lookup procedure, using association lists, is defined as follows, to be inserted by reflection. (The definition is in two parts, to avoid duplicating code. The first routine allows for environments to be represented either by association lists or by the original form of environments, to avoid having to scan the entire meta-tower system below the current point to convert all environments. It would be more typical of our reflective system to use an environment instead of a typecase, but that would make it more complicated to set up than is warranted for a presented example.)
(defun new-lookup (item env)
(typecase env
(environment
(lookup item env))
(list
(cdr (assoc item env)))))
This routine is analogous to the normal symbol lookup routine presented in section 7.3:
(defun new-symbol-lookup (symbol background-level)
(cond
((eq symbol t) t)
((keywordp (the symbol symbol))
symbol)
(t
(let ((dynamically-found
(new-lookup symbol
(level-dynamic-environment
background-level))))
(if dynamically-found
dynamically-found
(new-lookup symbol
(level-lexical-environment
background-level)))))))
and a binding procedure, also using association lists, is defined:
(defun new-bind (name environment value) (cons (cons name value) environment))
These are reflected in using something that calls the following procedure. First, it takes apart the data structures used, and saves the old values in variables:
(defun eval-with-typevals-and-ops (level
typeval-bindings
opbindings
form)
(let ((the-closure (level-current-closure level))
(the-old-language (closure-language the-closure))
(the-old-type-evaluators
(closure-type-evaluators the-closure))
(the-language (copy-language the-old-language))
(the-type-evaluators
(copy-language the-old-type-evaluators)))
(set-closure-language the-closure the-language)
then it adds new bindings in the language and
type-evaluators environments:
(dolist (this-binding opbindings)
(let ((opname (car this-binding))
(opform (cdr this-binding)))
(bind opname the-language opform)))
(dolist (this-binding typeval-bindings)
(let ((tyname (car this-binding))
(tyform (cdr this-binding)))
(bind tyname the-type-evaluators tyform)))
After that, it evaluates its argument form, and
restores the old values of the language and
type-evaluator environments:
(let ((result (eval-in-level form level)))
(set-closure-language
the-closure
the-old-language)
(set-closure-type-evaluators
the-closure
the-old-type-evaluators)
result)))
This provides a general facility for any reflective changes that modify the handling of a particular type of sub-expression or other value; these changes often require both alterations to the evaluator and to existing operators, and also possibly the addition of some new operators.
To use this for changing the implementation of non-local variables, it is called from the following procedure:
(defun eval-with-alternate-bindings-by-type-evals (form)
(progn
(eval-with-typevals-and-ops
(current-level)
'( (symbol . new-symbol-lookup) )
'( (lookup . new-lookup) )
(cons 'eval-with-alternate-environment-representation
(cons form nil)))))
This constructs a form to evaluate its original
argument form using
'eval-with-alternate-environment-representation, which
converts the environments between the two
representations:
(defun eval-with-alternate-environment-representation (form)
(progn
(let ((closure (level-current-closure (current-level)))
(old-lex-env (closure-lexical-environment closure))
(new-lex-env (environment-to-alist old-lex-env))
(old-dyn-env (closure-fluid-environment closure))
(new-dyn-env (environment-to-alist old-dyn-env)))
(set-closure-lexical-environment closure new-lex-env)
(set-closure-fluid-environment closure new-dyn-env)
(let ((res (eval form)))
(set-closure-lexical-environment closure old-lex-env)
(set-closure-fluid-environment closure old-dyn-env)
res))))
In Platypus, evaluation order is largely defined by the operator definitions, which call the evaluator to evaluate each argument at the appropriate point. It is, in principle, possible to write an evaluator that normally returns lazy results, probably as closures to be evaluated later (or on a separate computer, to provide parallelism; see [Halstead 85], Kranz et al 89, [Miller 87], [Osborne89]) and which evaluates things only when necessary. However, because Platypus's model of evaluation allows side-effects anywhere (including the very general side-effect of jumpy reflection, as described in section 9.4), this does not in itself provide a universal means for lazifying any existing language! It could, however, be used to implement languages known not to allow side-effects.
It is possible to get round the problem of implementing languages with side-effects, using the power and flexibility of an interpretive system based upon metacontinuations. This may be done by returning lazy results (futures) but keeping a list of them (that is, of futures that need further evaluation to become proper values) in a variable of the evaluator of the level above that containing the lazified program. Whenever a side-effect is about to occur (the evaluator must monitor for this, by catching all use of primitive (shadowed) operators that can produce side-effects) all the stored lazy results are evaluated further toward their real results, and any that finish their evaluation can be dropped from this list. This way, consistency is guaranteed when side-effects happen, although the system is otherwise lazy.
If a lazy evaluator were installed at some level in the tower, all levels below that would become lazy, as no evaluation would occur there until needed. This is an example of how changes at one level may be pervasive through to all lower levels (which have no control over the matter---see section 5.3).
Some languages, particularly those that are primarily part of a special-purpose system, and only secondarily programming languages (for example, expansion languages for programmable text editors, and graphics languages such as PostScript, require special features in their implementations that would not be present in more general-purpose languages. For example, an editor language typically will have one or more buffers in which to hold text, each with a current point, and PostScript has a current graphics state (transformation, colour, linewidth, etc), and usually an underlying imaging system for painting onto a bitmap.
What is the most appropriate place to store such special substrate data? It is not in named variables at the application program level---the namespace must be kept clear for the application program to use in its entirity---but neither may it make the generic evaluator become specialized. The solution is to put it at the evaluator's level, using variables named by agreement between the operators concerned (such as editor-specific or graphics-specific operators)---observe in the code at section 7.3 that the core evaluator routines do not use any non-local variables at their own level.
Some languages require features that are difficult to integrate with the rest of the system---for example, PostScript's access permission flags which are a part of each of its [compound?] values. Theoretically, this could be implemented tidily by changing the substrate on which the evaluator runs, so that the evaluator works in a world with the relevant underlying type system, but this does not seem very practical. For most purposes, such incompatibilities seem quite minor, and often it may be simplest to tolerate them---for example, to say that all values always allow reading and writing. (In the trial implementation of PostScript in Platypus, we cheat, through good chance, on PostScript's executable and non-executable (literal) arrays, by representing them as arrays and expressions (Lisp lists) respectively---thus mapping a non-standard distinction onto a standard one not otherwise made by that language.)
The need for such substrate features is often connected with the need for special types of value. For such types, it may be appropriate to compile procedures for handling their values, as described in section 13.2.
Our mixed-language interpretation is designed to allow many languages to be built on top of it. Languages which can be converted readily to a procedural form are most suitable for this: procedural and functional languages are easiest, declarative and rule-based languages are harder.
We assume handling of such types as numbers to be made available underneath the implementation of reflection. Reflection does not help to describe these, anyway, so nothing would be gained were it possible to include them in the reflective system.
Most conventional language features map readily onto a reflective mixed-language architecture. Occasionally there is a mismatch, such as it being natural to try to make all calls reflective (which builds a tower level for each procedure call).
Using jumpy reflectors (that assign to parts of the state, without saving the old values on a stack) to change specific parts of a tower allows very natural implementation of many common language features such as jumps, calls and assignments.
Reflective features may be used to group together parts of a system, such as all the operators of a language, for interpretation in a particular way.
As well as any languages implemented on top of the reflective system, there is a base language which provides reflective facilities and some simple flow control and calling operators. This is sufficient for running the rest of the system, so long as all parts of the system are connected with integrity to the base language.
Reflection allows new features to be added to conventional languages, including extreme examples such as a non-local exit that goes right out of several levels of interpretation.
Procedure calls are to some extent built into the evaluator, but other features are not so much so. Our procedure calling is naturally call-by-name, but call-by-value may be implemented easily on top of this; such a facility is provided in a form that is useful to many language implementations.
``
Must a name mean something?'' Alice asked doubtfully.``Of course it must'' Humpty Dumpty said with a short laugh.
Alice Through the Looking Glass, Chapter 6