A model meta-evaluator

Having already described the standard interpreter we now look at a model for the meta-evaluator. The meta-evaluator stands in for an infinite string of meta-circular standard interpreter levels, and in so doing implements the entire first dimension of the tower. To do so, whenever it is about to call a procedure---whether that is the evaluator, a type-evaluator or an operator---which is shadowed, it must call the shadow procedure (which runs in the meta-evaluator's own level, but performs actions as though it were in the meta-evaluatee's level) instead of the original procedure.

Requirements for the meta-evaluator

There are two major requirements for the meta-evaluator:

• it must be able to do everything that the standard interpreter can do;
• it must support level-shifting within its own level, in such a way that it can realize on demand levels for use in the tower that it implements.

Since we are not requiring it to conform to the structure of a tower level itself, we can observe that

• it may be a whole interpreter (evaluator and language in one);
• it must provide operations on the fundamental types on which the standard interpreter's type system is based.

Most of the operations of the meta-evaluator will be directly equivalent to those of the standard interpreter, and the forms of the two will be similar. Reflective operations do not translate so directly into operations of the meta-evaluator because they do level-shifting, which is not possible when there is only one level. The operations which cause level-shifts in the standard interpreter must translate to non-reflective actions in the meta-evaluator.

Thus, we have the mappings:

• Non-Reflective Actions Non-Reflective Actions
• Reflective Actions Non-Reflective Actions

All these actions affect variables of the meta-evaluator, which represent the state of the tower. The meta-evaluator has one important variable, let us call it *tower*, whose value is the tower which it interprets. This is the argument with which the meta-evaluator was called.

A non-reflective operation in the tower works on the contents of the base of the tower. For example, arithmetic operators handle values in the values element of the current closure at the lowest level of the tower, and flow control operators affect the stack of sub-functions (sub-expressions) implicit in the expressions elements of the stack of closures at that level.

Reflective operations may change the contents of the tower more significantly. For example, the grand-jumpy-reflector operation sets *tower* to a fresh value that has been produced from somewhere within the (old) contents of *tower*. Likewise, grand-jumpy-reifier assigns to a location (such as the value part of a variable binding) stored within the current value of *tower*. These may be used, in conjunction with a stack in the meta-evaluator, to implement pushy reflection.

This description would suffice were the meta-evaluator to be positioned at the end of the tower. A lightning bolt [Smith 82] is needed to reach from the top of the tower (where the ground is) toward the base of the tower. This must cut through the infinite repetitive (boring) section of the tower:

However, as well as being at the infinitely remote upper end of the tower, the meta-evaluator has to be alongside the whole tower, so that it can reach through the infinite section of the tower, to shadow things at the lowest level at which it is possible:

The lightning here travels along the tower through the meta-evaluator, which can conduct it from one level to another as needed. As already discussed, it strikes the highest point on the tower that is not mimicked by the meta-evaluator; before this, it is just travelling through open space, and does not touch anything.

Because of the meta-evaluator being beside the tower, its connection to the tower is more complicated. Indeed the tower is more complicated than that, as it has a castle of towers arising from the operator closures in the language of each level, thus:

The following diagram shows that the meta-evaluator is alongside everything, and that it contacts (shadows) any tower in the castle wherever a tower in that tree reaches meta-circular standard interpretation:

An introduction to platypus

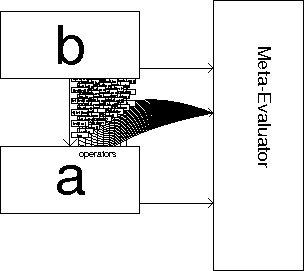
Platypus is a non-reflective, single-language implementation of a reflective, mixed-language interpreter. (Its name originally stood for Practical Language Algebra with TYpes, Procedures, Unification and Sending, although the latter two features are not implemented in this version of it.)

There are now three implementations of Platypus: an early prototype written in Cambridge Lisp, a version in C written for speed, and a more readable and concise version in Common Lisp. Both of the latter two are referred to below. Example code throughout the thesis is drawn largely from the Common Lisp implementation, Platypus89.

Platypus is a shadowing interpreter, as described in sections shadowidea and shadowint, and has to implement:

• all the operators needed in the standard interpreter that it mimics;
• level-shifting, including the creation of new levels on demand;
• auxiliary functions, such as storage management, input and output.

The pull of efficiency

My thesis is that the reflective facilities described can be implemented efficiently enough (compared against a conventional system) that a programming system using them is useable in practice, at least for prototyping. Hence the intensively used parts of Platypus are written with efficiency in mind. It is also essential that everything required in the reflective system is provided correctly---correctness cannot be compromised to gain speed. Therefore, there is a division of Platypus' internals into two parts:

• those that are mapped onto by the standard interpreter: these are visible and hence have to fit exactly to the abstract model of interpretation used by Platypus;
• those that are private to the meta-evaluator: these are not visible to programs running on the system, and so can be implemented with any programming techniques that will provide enough speed.

This division is particularly noticeable in the C version. In Platypus89, the equivalent procedures inside and outside the tower could be produced from the same source, with one branch being held as a lambda-expression inside the tower, and the other compiled to machine code by the substrate Lisp system. (In practice, the sources are similar but not identical for most of the code, for historical reasons. Some of the compiled code is generated mechanically from the non-compiled code definitions, particularly for Lisp-like functions that evaluate all of their arguments.)

Representation strategies

There are two ways in which we could store tower components:

• in exactly the form in which they are seen through reifiers;
• in a form convenient to the meta-evaluator, which must be converted to and from the form seen within the tower.

In all versions of Platypus, to be sure of the correct representation of reified state to the application, we use the former approach: everything is pre-reified---only ever kept in its reified form---rather than reified on demand. This means we that have to write the meta-evaluator to handle all the reifiable structures in their reified form throughout. The only values which are not always kept in a reified form are those that have no reified form, such as the internals of file stream descriptors.

In practice, it turns out that this works well; representations suitable for use with reified data are also suitable for use by the evaluator and meta-evaluator, and there are no points at which some other representation would have been obviously more suitable.

However, were translation at reification and reflection to be used, it would occur at very specific points (the reifiers and reflectors). Much of it would be simple, although there are possibilities for complicated reifiers and reflectors, ranging from building of reified stack frames to de-compilation at reification and compilation at reflection [Watson And Tillotson 89]. Because of the translation occuring at such well-defined places, the possibilities for errors introduced by this feature are restricted, and the possible effects on the rest of the system are reduced.

Mapping

Objects in the tower world that have special meaning to the meta-evaluator, such as the closures representing functions which the meta-evaluator evaluates directly itself, must be mapped onto the corresponding objects in the meta-evaluator. In the C implementation of Platypus, this mapping is done by a pair of hash tables, using a perfect hashing scheme---that is, hash table lookups take a constant time. This is made possible by special allocation of memory while initializing the system (see section 11.7), such that there is something special about the addresses of the heap objects that have special meanings to the meta-evaluator.

The more significant of the two hash tables in the C implementation, as far as reflective interpretation is concerned, is the operator map. This maps from objects inside the tower to functions in the meta-evaluator. If the object is a closure representing a primitive operator, that is, one which is shadowed by the meta-evaluator, and is being called from the standard evaluator, this mapping succeeds and returns the meta-evaluator function. If the object is not a primitive operator closure, it is mapped to a distinguished null value.

The other hash table, called the location map, is concerned with garbage collection. It is used to update C variables pointing to distinguished heap objects (such as nil) as the garbage collector moves things around.

In the Common Lisp implementation, Platypus89, the hashing for the operator map is done by normal Lisp hash-tables. There is no location map in this implementation, as we use Lisp's garbage collector, and all levels share one conceptual undivided address space (and type space!), and so our meta-evaluator variables pointing into the tower are updated automatically as part of the normal action of Lisp's garbage collector.

The meaning of the map

As mentioned in section 10.6, the operator map is in some ways analagous to a language. Just as a language maps operator names (which are symbols, or tokens) to operator closures, the operator map maps operator closures at one meta-level to those at another.

Now, since the meaning of a name is not inherent in the name, but only in the context (environment) in which the name is de-referenced, any kind of value (such as an operator closure) may be used as a name. Thus, both operator maps and languages translate operator names (operator extensions) of some kind to operator closures (operator intensions) so that the intension of the operator may be used to fulfil, in that context, the extension of the operator.

How the meta-evaluator works

Meta-circular calls to the standard interpreter are recognized with a single comparison operation. When the meta-evaluator begins to evaluate a level, it compares the evaluator of that level with the standard evaluator.

• If they are the same, the meta-evaluator evaluates the level itself;
• If they are different, the meta-evaluator builds a new real tower level in which to run the evaluator of the level with the level as the argument to the evaluator. (The new level was already there in principle, but was not realized in memory). The meta-evaluator then recurses to evaluate this level.

When the meta-evaluator is interpreting a level directly, each time it tries to apply an operator or type-evaluator, on behalf of a standard interpreter level which it is shadowing, it first looks it up in the appropriate map.

• If it finds the null value (that is, the operator or type-evaluator is not mapped), it climbs the tower, by realizing a new level of the tower to run the evaluator of that operator or type-evaluator, and recursing to interpret it;
• If it finds a non-null value, it calls the shadow function (in the language of the implementation) denoted by that value, with the current level as its argument. The whole tower is accessible through this level, since each level has its evaluator built into its structure, and holds its evaluee, if any, in the argument list of its current closure.

This is almost identical to the action of the standard interpreter within the tower, except that there is a conditional level-shift in a one-level-deep second tower dimension, and when this level shift is taken, the operator or type-evaluator shadowing map is used much like a language.

The actions of the C and Lisp implementations are very similar. As far as the ideas of reflective interpretation are concerned, they are equivalent. In the implementations, the main difference between the evaluators is in the mapping mechanism---and this is a small difference, and in either implementation, it could be done some other way. The most notable difference between the substrate systems is that Lisp provides a lot of useful things (such as memory management) that had to be written into the C version directly.

Summary of the model meta-evaluator

``And part of the roof came off, and ever so much thunder got in---and it went rolling round the room in great lumps---and knocking over the tables and things---till I was so frightened, I couldn't remember my own name!''

The White Queen, Alice Through the Looking Glass, Chapter 9

Footnotes